Menu Close

d-sin-2-sin-3-sin-5-

Tinku Tara 0 Comments
Pin




Question Number 39230 by MJS last updated on 04/Jul/18
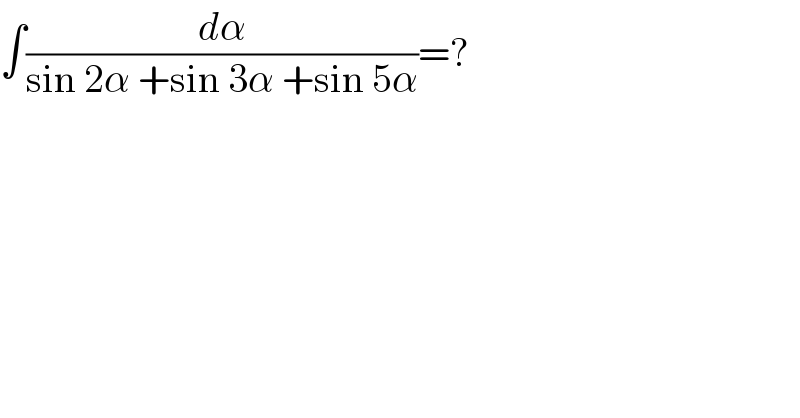
∫(dα/(sin 2α +sin 3α +sin 5α))=?
$$\int\frac{{d}\alpha}{\mathrm{sin}\:\mathrm{2}\alpha\:+\mathrm{sin}\:\mathrm{3}\alpha\:+\mathrm{sin}\:\mathrm{5}\alpha}=? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Jul/18
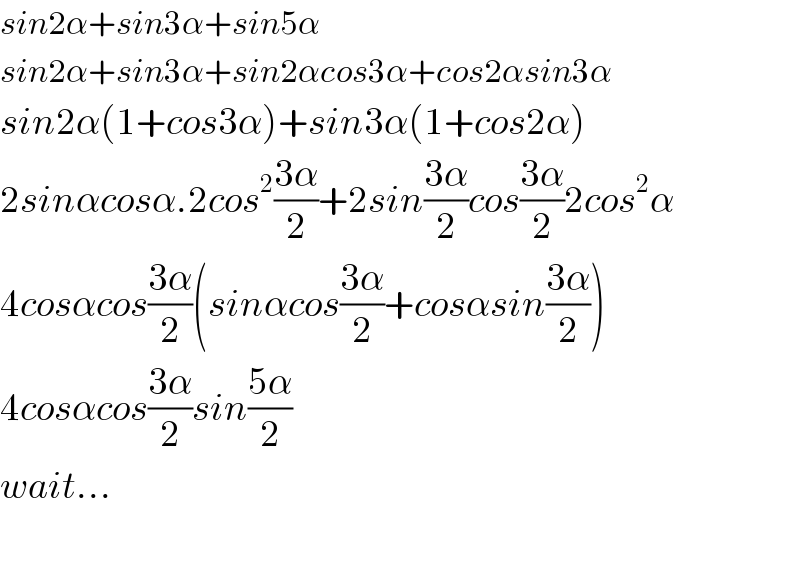
sin2α+sin3α+sin5α sin2α+sin3α+sin2αcos3α+cos2αsin3α sin2α(1+cos3α)+sin3α(1+cos2α) 2sinαcosα.2cos^2 ((3α)/2)+2sin((3α)/2)cos((3α)/2)2cos^2 α 4cosαcos((3α)/2)(sinαcos((3α)/2)+cosαsin((3α)/2)) 4cosαcos((3α)/2)sin((5α)/2) wait...
$${sin}\mathrm{2}\alpha+{sin}\mathrm{3}\alpha+{sin}\mathrm{5}\alpha \\ $$$${sin}\mathrm{2}\alpha+{sin}\mathrm{3}\alpha+{sin}\mathrm{2}\alpha{cos}\mathrm{3}\alpha+{cos}\mathrm{2}\alpha{sin}\mathrm{3}\alpha \\ $$$${sin}\mathrm{2}\alpha\left(\mathrm{1}+{cos}\mathrm{3}\alpha\right)+{sin}\mathrm{3}\alpha\left(\mathrm{1}+{cos}\mathrm{2}\alpha\right) \\ $$$$\mathrm{2}{sin}\alpha{cos}\alpha.\mathrm{2}{cos}^{\mathrm{2}} \frac{\mathrm{3}\alpha}{\mathrm{2}}+\mathrm{2}{sin}\frac{\mathrm{3}\alpha}{\mathrm{2}}{cos}\frac{\mathrm{3}\alpha}{\mathrm{2}}\mathrm{2}{cos}^{\mathrm{2}} \alpha \\ $$$$\mathrm{4}{cos}\alpha{cos}\frac{\mathrm{3}\alpha}{\mathrm{2}}\left({sin}\alpha{cos}\frac{\mathrm{3}\alpha}{\mathrm{2}}+{cos}\alpha{sin}\frac{\mathrm{3}\alpha}{\mathrm{2}}\right) \\ $$$$\mathrm{4}{cos}\alpha{cos}\frac{\mathrm{3}\alpha}{\mathrm{2}}{sin}\frac{\mathrm{5}\alpha}{\mathrm{2}} \\ $$$${wait}… \\ $$$$ \\ $$
Answered by MJS last updated on 04/Jul/18
sin 2α =2sin α cos α sin 3α =3sin α cos^2 α −sin^3 α sin 5α =sin^5 α −10sin^3 α cos^2 α +5sin α cos^4 α sin 2α +sin 3α +sin 5α = 2sc+3sc^2 −s^3 +s^5 −10s^3 c^2 +5sc^4 = =2sc+s(3c^2 −s^2 +s^4 −10s^2 c^2 +5c^4 )= =2sc+s(3c^2 −(1−c^2 )+(1−c^2 )^2 −10(1−c^2 )c^2 +5c^4 )= =2sc+8sc^2 (2c^2 −1)=2((s^2 c+4s^2 c^2 (2c^2 −1))/s)= =2(((1−c^2 )c+4(1−c^2 )c^2 (2c^2 −1))/s)= =−2(((4c^2 +2c−1)(2c−1)(c−1)(c+1)c)/s) ∫(dα/(sin 2α +sin 3α +sin 5α))= =−(1/2)∫((sin α)/((4cos^2 α +2cos α −1)(2cos α −1)(cos α −1)(cos α +1)cos α))dα= [t=cos α → dα=−(dt/(sin α))] =(1/2)∫(dt/((4t^2 +2t−1)(2t−1)(t−1)(t+1)t))= =(1/2)∫((C_1 /t)+(C_2 /(t−1))+(C_3 /(t+1))+(C_4 /(2t−1))+(C_5 /(2t+((1−(√5))/2)))+(C_6 /(2t+((1+(√5))/2))))dt= [C_1 =−1; C_2 =(1/(10)); C_3 =−(1/6); C_4 =−(8/3); C_5 =((12+4(√5))/5); C_6 =((12−4(√5))/5)] =−(1/2)∫(dt/t)+(1/(20))∫(dt/(t−1))−(1/(12))∫(dt/(t+1))−(2/3)∫(dt/(t−(1/2)))+((3+(√5))/5)∫(dt/(t+((1−(√5))/4)))+((3−(√5))/5)∫(dt/(t+((1+(√5))/4)))= =−(1/2)ln∣t∣+(1/(20))ln∣t−1∣−(1/(12))ln∣t+1∣−(2/3)ln∣t−(1/2)∣+((3+(√5))/5)ln∣t+((1−(√5))/4)∣+((3−(√5))/5)ln∣t+((1+(√5))/4)∣= =−(1/2)ln∣cos α∣+(1/(20))ln∣cos α −1∣−(1/(12))ln∣cos α +1∣−(2/3)ln∣cos α −(1/2)∣+((3+(√5))/5)ln∣cos α +((1−(√5))/4)∣+((3−(√5))/5)ln∣cos α +((1+(√5))/4)∣+C
$$\mathrm{sin}\:\mathrm{2}\alpha\:=\mathrm{2sin}\:\alpha\:\mathrm{cos}\:\alpha \\ $$$$\mathrm{sin}\:\mathrm{3}\alpha\:=\mathrm{3sin}\:\alpha\:\mathrm{cos}^{\mathrm{2}} \:\alpha\:−\mathrm{sin}^{\mathrm{3}} \:\alpha \\ $$$$\mathrm{sin}\:\mathrm{5}\alpha\:=\mathrm{sin}^{\mathrm{5}} \:\alpha\:−\mathrm{10sin}^{\mathrm{3}} \:\alpha\:\mathrm{cos}^{\mathrm{2}} \:\alpha\:+\mathrm{5sin}\:\alpha\:\mathrm{cos}^{\mathrm{4}} \:\alpha \\ $$$$\mathrm{sin}\:\mathrm{2}\alpha\:+\mathrm{sin}\:\mathrm{3}\alpha\:+\mathrm{sin}\:\mathrm{5}\alpha\:= \\ $$$$\mathrm{2}{sc}+\mathrm{3}{sc}^{\mathrm{2}} −{s}^{\mathrm{3}} +{s}^{\mathrm{5}} −\mathrm{10}{s}^{\mathrm{3}} {c}^{\mathrm{2}} +\mathrm{5}{sc}^{\mathrm{4}} = \\ $$$$=\mathrm{2}{sc}+{s}\left(\mathrm{3}{c}^{\mathrm{2}} −{s}^{\mathrm{2}} +{s}^{\mathrm{4}} −\mathrm{10}{s}^{\mathrm{2}} {c}^{\mathrm{2}} +\mathrm{5}{c}^{\mathrm{4}} \right)= \\ $$$$=\mathrm{2}{sc}+{s}\left(\mathrm{3}{c}^{\mathrm{2}} −\left(\mathrm{1}−{c}^{\mathrm{2}} \right)+\left(\mathrm{1}−{c}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{10}\left(\mathrm{1}−{c}^{\mathrm{2}} \right){c}^{\mathrm{2}} +\mathrm{5}{c}^{\mathrm{4}} \right)= \\ $$$$=\mathrm{2}{sc}+\mathrm{8}{sc}^{\mathrm{2}} \left(\mathrm{2}{c}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{2}\frac{{s}^{\mathrm{2}} {c}+\mathrm{4}{s}^{\mathrm{2}} {c}^{\mathrm{2}} \left(\mathrm{2}{c}^{\mathrm{2}} −\mathrm{1}\right)}{{s}}= \\ $$$$=\mathrm{2}\frac{\left(\mathrm{1}−{c}^{\mathrm{2}} \right){c}+\mathrm{4}\left(\mathrm{1}−{c}^{\mathrm{2}} \right){c}^{\mathrm{2}} \left(\mathrm{2}{c}^{\mathrm{2}} −\mathrm{1}\right)}{{s}}= \\ $$$$=−\mathrm{2}\frac{\left(\mathrm{4}{c}^{\mathrm{2}} +\mathrm{2}{c}−\mathrm{1}\right)\left(\mathrm{2}{c}−\mathrm{1}\right)\left({c}−\mathrm{1}\right)\left({c}+\mathrm{1}\right){c}}{{s}} \\ $$$$ \\ $$$$\int\frac{{d}\alpha}{\mathrm{sin}\:\mathrm{2}\alpha\:+\mathrm{sin}\:\mathrm{3}\alpha\:+\mathrm{sin}\:\mathrm{5}\alpha}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{sin}\:\alpha}{\left(\mathrm{4cos}^{\mathrm{2}} \:\alpha\:+\mathrm{2cos}\:\alpha\:−\mathrm{1}\right)\left(\mathrm{2cos}\:\alpha\:−\mathrm{1}\right)\left(\mathrm{cos}\:\alpha\:−\mathrm{1}\right)\left(\mathrm{cos}\:\alpha\:+\mathrm{1}\right)\mathrm{cos}\:\alpha}{d}\alpha= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{cos}\:\alpha\:\rightarrow\:{d}\alpha=−\frac{{dt}}{\mathrm{sin}\:\alpha}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\left(\mathrm{4}{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}\right)\left(\mathrm{2}{t}−\mathrm{1}\right)\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right){t}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{{C}_{\mathrm{1}} }{{t}}+\frac{{C}_{\mathrm{2}} }{{t}−\mathrm{1}}+\frac{{C}_{\mathrm{3}} }{{t}+\mathrm{1}}+\frac{{C}_{\mathrm{4}} }{\mathrm{2}{t}−\mathrm{1}}+\frac{{C}_{\mathrm{5}} }{\mathrm{2}{t}+\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}}+\frac{{C}_{\mathrm{6}} }{\mathrm{2}{t}+\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}}\right){dt}= \\ $$$$\:\:\:\:\:\left[{C}_{\mathrm{1}} =−\mathrm{1};\:{C}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{10}};\:{C}_{\mathrm{3}} =−\frac{\mathrm{1}}{\mathrm{6}};\:{C}_{\mathrm{4}} =−\frac{\mathrm{8}}{\mathrm{3}};\:{C}_{\mathrm{5}} =\frac{\mathrm{12}+\mathrm{4}\sqrt{\mathrm{5}}}{\mathrm{5}};\:{C}_{\mathrm{6}} =\frac{\mathrm{12}−\mathrm{4}\sqrt{\mathrm{5}}}{\mathrm{5}}\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{t}}+\frac{\mathrm{1}}{\mathrm{20}}\int\frac{{dt}}{{t}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{12}}\int\frac{{dt}}{{t}+\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{dt}}{{t}−\frac{\mathrm{1}}{\mathrm{2}}}+\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{5}}\int\frac{{dt}}{{t}+\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}}}+\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{5}}\int\frac{{dt}}{{t}+\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid{t}\mid+\frac{\mathrm{1}}{\mathrm{20}}\mathrm{ln}\mid{t}−\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{12}}\mathrm{ln}\mid{t}+\mathrm{1}\mid−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\mid{t}−\frac{\mathrm{1}}{\mathrm{2}}\mid+\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{5}}\mathrm{ln}\mid{t}+\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}}\mid+\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{5}}\mathrm{ln}\mid{t}+\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\mid= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{cos}\:\alpha\mid+\frac{\mathrm{1}}{\mathrm{20}}\mathrm{ln}\mid\mathrm{cos}\:\alpha\:−\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{12}}\mathrm{ln}\mid\mathrm{cos}\:\alpha\:+\mathrm{1}\mid−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\mid\mathrm{cos}\:\alpha\:−\frac{\mathrm{1}}{\mathrm{2}}\mid+\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{5}}\mathrm{ln}\mid\mathrm{cos}\:\alpha\:+\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}}\mid+\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{5}}\mathrm{ln}\mid\mathrm{cos}\:\alpha\:+\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\mid+{C} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 04/Jul/18
excellent...its a proof of patience...
$${excellent}…{its}\:{a}\:{proof}\:{of}\:{patience}… \\ $$
Commented by MJS last updated on 04/Jul/18
corrected
$$\mathrm{corrected} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *