Question Number 91622 by Ar Brandon last updated on 02/May/20

$$\frac{\mathrm{d}\left(\mathrm{x}!\right)}{\mathrm{dx}}= \\ $$
Commented by MJS last updated on 02/May/20
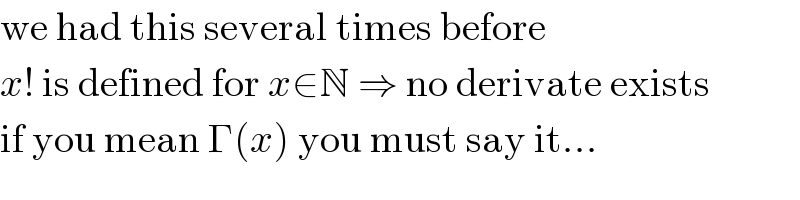
$$\mathrm{we}\:\mathrm{had}\:\mathrm{this}\:\mathrm{several}\:\mathrm{times}\:\mathrm{before} \\ $$$${x}!\:\mathrm{is}\:\mathrm{defined}\:\mathrm{for}\:{x}\in\mathbb{N}\:\Rightarrow\:\mathrm{no}\:\mathrm{derivate}\:\mathrm{exists} \\ $$$$\mathrm{if}\:\mathrm{you}\:\mathrm{mean}\:\Gamma\left({x}\right)\:\mathrm{you}\:\mathrm{must}\:\mathrm{say}\:\mathrm{it}… \\ $$
Answered by M±th+et+s last updated on 02/May/20
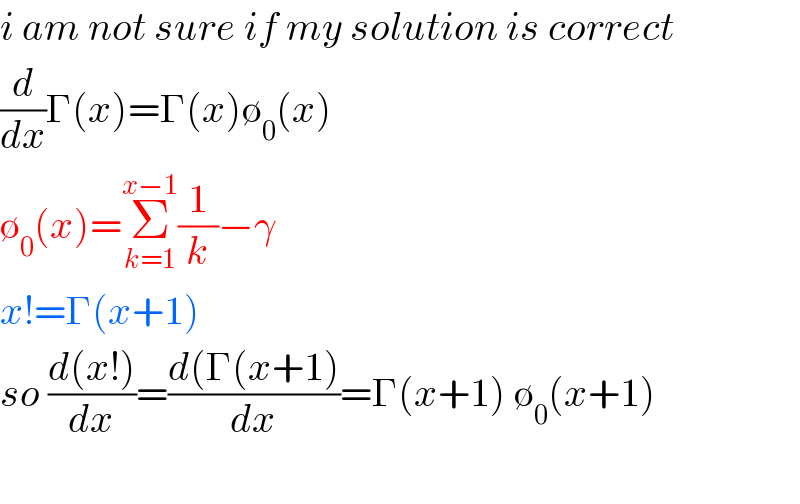
$${i}\:{am}\:{not}\:{sure}\:{if}\:{my}\:{solution}\:{is}\:{correct}\: \\ $$$$\frac{{d}}{{dx}}\Gamma\left({x}\right)=\Gamma\left({x}\right)\emptyset_{\mathrm{0}} \left({x}\right) \\ $$$$\emptyset_{\mathrm{0}} \left({x}\right)=\underset{{k}=\mathrm{1}} {\overset{{x}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{k}}−\gamma \\ $$$${x}!=\Gamma\left({x}+\mathrm{1}\right)\:\:\:\:\: \\ $$$${so}\:\frac{{d}\left({x}!\right)}{{dx}}=\frac{{d}\left(\Gamma\left({x}+\mathrm{1}\right)\right.}{{dx}}=\Gamma\left({x}+\mathrm{1}\right)\:\emptyset_{\mathrm{0}} \left({x}+\mathrm{1}\right) \\ $$$$ \\ $$
Answered by Ar Brandon last updated on 02/May/20

