Question Number 168819 by AbdoulayeLelouche last updated on 18/Apr/22
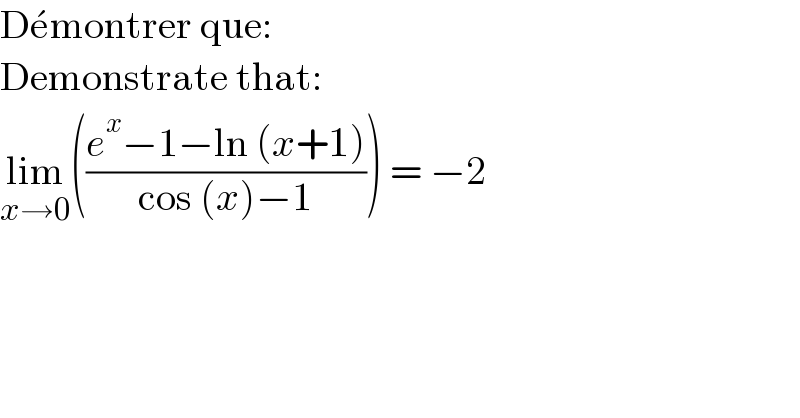
$$\mathrm{D}\acute {\mathrm{e}montrer}\:\mathrm{que}: \\ $$$$\mathrm{Demonstrate}\:\mathrm{that}: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{e}^{{x}} −\mathrm{1}−\mathrm{ln}\:\left({x}+\mathrm{1}\right)}{\mathrm{cos}\:\left({x}\right)−\mathrm{1}}\right)\:=\:−\mathrm{2} \\ $$
Answered by alephzero last updated on 18/Apr/22

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} −\mathrm{1}−\mathrm{ln}\left({x}+\mathrm{1}\right)}{\mathrm{cos}\:{x}−\mathrm{1}}\:= \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{d}}{{dx}}\left({e}^{{x}} −\mathrm{1}−\mathrm{ln}\left({x}+\mathrm{1}\right)\right)}{\frac{{d}}{{dx}}\left(\mathrm{cos}\:{x}−\mathrm{1}\right)}\:= \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} −\frac{\mathrm{1}}{{x}+\mathrm{1}}}{−\mathrm{sin}\:{x}}\:=\:−\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{{d}}{{dx}}\left({e}^{{x}} −\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)}{\frac{{d}}{{dx}}\left(\mathrm{sin}\:{x}\right)} \\ $$$$=\:−\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} +\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }}{\mathrm{cos}\:{x}}\:= \\ $$$$=\:−\frac{{e}^{\mathrm{0}} +\frac{\mathrm{1}}{\left(\mathrm{0}+\mathrm{1}\right)^{\mathrm{2}} }}{\mathrm{cos}\:\mathrm{0}}\:=\:−\frac{\mathrm{1}+\mathrm{1}}{\mathrm{1}}\:=\:−\mathrm{2}\:\blacksquare \\ $$
Commented by AbdoulayeLelouche last updated on 20/Apr/22
$$\mathrm{thanks}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much} \\ $$
Answered by qaz last updated on 18/Apr/22
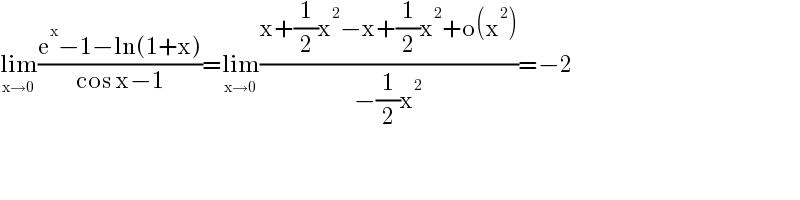
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{1}−\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{cos}\:\mathrm{x}−\mathrm{1}}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right)}{−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} }=−\mathrm{2} \\ $$
Commented by AbdoulayeLelouche last updated on 20/Apr/22
$$\mathrm{thanks}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much} \\ $$
Answered by chhaythean last updated on 18/Apr/22
![without L′hospital rule: =−lim_(x→0) ((e^x −x−1−[ln(1+x)−x])/(1−cosx)) =−lim_(x→0) (((e^x −x−1)/x^2 )/((1−cosx)/x^2 ))+lim_(x→0) (((ln(1+x)−x)/x^2 )/((1−cosx)/x^2 ))=A+B A=−lim_(x→0) (((e^x −x−1)/x^2 )/((1−cosx)/x^2 ))=−lim_(x→0) ((1/2)/(((2sin^2 ((x/2)))/(x^2 /4))×(1/4))) A=−lim_(x→0) ((1/2)/(1/2))=−1 B=lim_(x→0) (((ln(1+x)−x)/x^2 )/((1−cosx)/x^2 )) For: lim_(x→0) ((ln(1+x)−x)/x^2 ) let y=ln(1+x)⇒x=e^y −1 =lim_(y→0) ((−e^y +1+y)/((e^y −1)^2 ))=−lim_(y→0) ((e^y −y−1)/y^2 )×(y^2 /((e^(y−1) )^2 ))=−(1/2) ⇒B=lim_(x→0) (((ln(1+x)−x)/x^2 )/((1−cosx)/x^2 ))=((−(1/2))/(1/2))=−1 ⇒lim_(x→0) ((e^x −1−ln(x+1))/(cosx−1))= determinant (((−2))) Note: L=lim_(x→0) ((e^x −x−1)/x^2 ) let x=2y =lim_(y→0) ((e^(2y) −y−1)/(4y^2 ))=(1/4)lim_(y→0) ((e^y −y−1)/y^2 )(e^y +y+1)+(1/4) L=(1/2)L+(1/4)⇒L=(1/2) ⇒ lim_(x→0) ((e^x −x−1)/x^2 )=(1/2)](https://www.tinkutara.com/question/Q168827.png)
$$\:\:\:\:\: \\ $$$$\mathrm{without}\:\mathrm{L}'\mathrm{hospital}\:\mathrm{rule}: \\ $$$$=−\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{x}−\mathrm{1}−\left[\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)−\mathrm{x}\right]}{\mathrm{1}−\mathrm{cosx}} \\ $$$$=−\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\frac{\mathrm{1}−\mathrm{cosx}}{\mathrm{x}^{\mathrm{2}} }}+\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)−\mathrm{x}}{\mathrm{x}^{\mathrm{2}} }}{\frac{\mathrm{1}−\mathrm{cosx}}{\mathrm{x}^{\mathrm{2}} }}=\mathrm{A}+\mathrm{B} \\ $$$$\mathrm{A}=−\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\frac{\mathrm{1}−\mathrm{cosx}}{\mathrm{x}^{\mathrm{2}} }}=−\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\mathrm{2sin}^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)}{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}}×\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\mathrm{A}=−\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{2}}}=−\mathrm{1} \\ $$$$\mathrm{B}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)−\mathrm{x}}{\mathrm{x}^{\mathrm{2}} }}{\frac{\mathrm{1}−\mathrm{cosx}}{\mathrm{x}^{\mathrm{2}} }} \\ $$$$\mathrm{For}:\:\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)−\mathrm{x}}{\mathrm{x}^{\mathrm{2}} }\:\mathrm{let}\:\mathrm{y}=\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\Rightarrow\mathrm{x}=\mathrm{e}^{\mathrm{y}} −\mathrm{1} \\ $$$$=\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{e}^{\mathrm{y}} +\mathrm{1}+\mathrm{y}}{\left(\mathrm{e}^{\mathrm{y}} −\mathrm{1}\right)^{\mathrm{2}} }=−\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{e}^{\mathrm{y}} −\mathrm{y}−\mathrm{1}}{\mathrm{y}^{\mathrm{2}} }×\frac{\mathrm{y}^{\mathrm{2}} }{\left(\mathrm{e}^{\mathrm{y}−\mathrm{1}} \right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{B}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)−\mathrm{x}}{\mathrm{x}^{\mathrm{2}} }}{\frac{\mathrm{1}−\mathrm{cosx}}{\mathrm{x}^{\mathrm{2}} }}=\frac{−\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{2}}}=−\mathrm{1} \\ $$$$\Rightarrow\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{1}−\mathrm{ln}\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{cosx}−\mathrm{1}}=\begin{array}{|c|}{−\mathrm{2}}\\\hline\end{array} \\ $$$$\mathrm{Note}:\:\mathrm{L}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{let}\:\mathrm{x}=\mathrm{2y} \\ $$$$=\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{e}^{\mathrm{2y}} −\mathrm{y}−\mathrm{1}}{\mathrm{4y}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}}\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{e}^{\mathrm{y}} −\mathrm{y}−\mathrm{1}}{\mathrm{y}^{\mathrm{2}} }\left(\mathrm{e}^{\mathrm{y}} +\mathrm{y}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{L}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{L}+\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow\mathrm{L}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by AbdoulayeLelouche last updated on 20/Apr/22
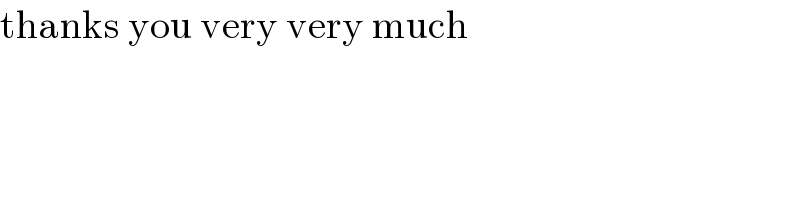
$$\mathrm{thanks}\:\mathrm{you}\:\mathrm{very}\:\mathrm{very}\:\mathrm{much} \\ $$
