Question Number 185625 by LEKOUMA last updated on 24/Jan/23

$${D}\acute {{e}terminer}\:{a},\:{b}\:{et}\:{c}\:{trois}\:{termes}\:{cons}\acute {{e}quences} \\ $$$${d}'{une}\:{suite}\:{g}\acute {{e}ometrique}\:{tels}\:{que}: \\ $$$$\begin{cases}{{a}+{b}+{c}=\mathrm{36},\mathrm{75}}\\{{abc}=\mathrm{343}}\end{cases} \\ $$
Answered by mr W last updated on 24/Jan/23
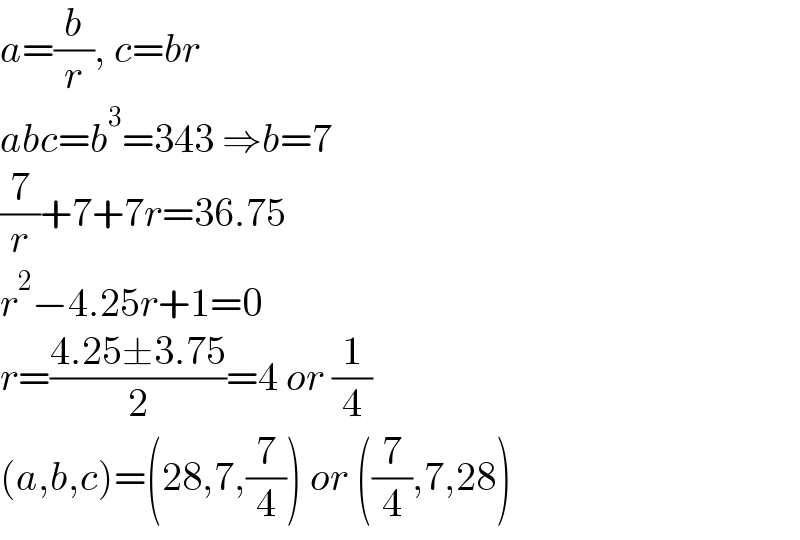
$${a}=\frac{{b}}{{r}},\:{c}={br} \\ $$$${abc}={b}^{\mathrm{3}} =\mathrm{343}\:\Rightarrow{b}=\mathrm{7} \\ $$$$\frac{\mathrm{7}}{{r}}+\mathrm{7}+\mathrm{7}{r}=\mathrm{36}.\mathrm{75} \\ $$$${r}^{\mathrm{2}} −\mathrm{4}.\mathrm{25}{r}+\mathrm{1}=\mathrm{0} \\ $$$${r}=\frac{\mathrm{4}.\mathrm{25}\pm\mathrm{3}.\mathrm{75}}{\mathrm{2}}=\mathrm{4}\:{or}\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\left({a},{b},{c}\right)=\left(\mathrm{28},\mathrm{7},\frac{\mathrm{7}}{\mathrm{4}}\right)\:{or}\:\left(\frac{\mathrm{7}}{\mathrm{4}},\mathrm{7},\mathrm{28}\right) \\ $$
