Question Number 87398 by jagoll last updated on 04/Apr/20
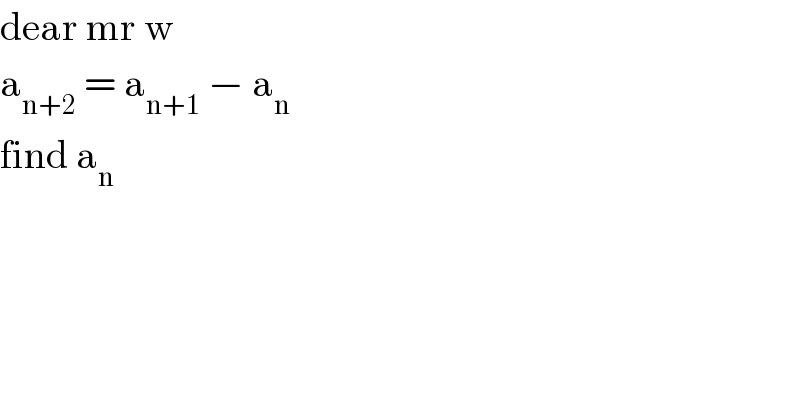
$$\mathrm{dear}\:\mathrm{mr}\:\mathrm{w} \\ $$$$\mathrm{a}_{\mathrm{n}+\mathrm{2}} \:=\:\mathrm{a}_{\mathrm{n}+\mathrm{1}} \:−\:\mathrm{a}_{\mathrm{n}} \\ $$$$\mathrm{find}\:\mathrm{a}_{\mathrm{n}} \\ $$
Commented by mr W last updated on 04/Apr/20

$${x}^{\mathrm{2}} −{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{1}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{cos}\:\frac{\pi}{\mathrm{3}}\pm{i}\:\mathrm{sin}\:\frac{\pi}{\mathrm{3}}={e}^{\pm{i}\frac{\pi}{\mathrm{3}}} \\ $$$$\Rightarrow{a}_{{n}} ={Ae}^{{i}\frac{{n}\pi}{\mathrm{3}}} +{Be}^{−{i}\frac{{n}\pi}{\mathrm{3}}} \\ $$$${you}\:{need}\:{to}\:{know}\:{a}_{\mathrm{1}} \:{and}\:{a}_{\mathrm{2}} \:{to}\:{determine} \\ $$$${A}\:{and}\:{B}. \\ $$
Commented by jagoll last updated on 04/Apr/20

$$\mathrm{given}\:\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\mathrm{1945}} {\sum}}\mathrm{a}_{\mathrm{n}} \:=\:\mathrm{2018}\:\mathrm{and}\: \\ $$$$\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\mathrm{2018}} {\sum}}\mathrm{a}_{\mathrm{n}} \:=\:\mathrm{1945}.\:\mathrm{Evaluate}? \\ $$$$\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\mathrm{2001}} {\sum}}\:\mathrm{a}_{\mathrm{n}} \:=\:? \\ $$
Commented by jagoll last updated on 04/Apr/20

$$\mathrm{how}\:\mathrm{to}\:\mathrm{get}\:\mathrm{A}\:\&\:\mathrm{B}\:\mathrm{sir}? \\ $$
Commented by mr W last updated on 04/Apr/20

$${a}_{{n}} ={Ae}^{{i}\frac{{n}\pi}{\mathrm{3}}} +{Be}^{−{i}\frac{{n}\pi}{\mathrm{3}}} ={Ap}^{{n}} +{Bq}^{{n}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{1945}} {\sum}}{a}_{{n}} ={A}\left(\underset{{n}=\mathrm{1}} {\overset{\mathrm{1945}} {\sum}}{p}^{{n}} \right)+{B}\left(\underset{{n}=\mathrm{1}} {\overset{\mathrm{1945}} {\sum}}{q}^{{n}} \right)=\mathrm{2018} \\ $$$$\Rightarrow\frac{{p}\left({p}^{\mathrm{1945}} −\mathrm{1}\right)}{{p}−\mathrm{1}}{A}+\frac{{q}\left({q}^{\mathrm{1945}} −\mathrm{1}\right)}{{q}−\mathrm{1}}{B}=\mathrm{2018} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{2018}} {\sum}}{a}_{{n}} ={A}\left(\underset{{n}=\mathrm{1}} {\overset{\mathrm{2018}} {\sum}}{p}^{{n}} \right)+{B}\left(\underset{{n}=\mathrm{1}} {\overset{\mathrm{2018}} {\sum}}{q}^{{n}} \right)=\mathrm{1945} \\ $$$$\Rightarrow\frac{{p}\left({p}^{\mathrm{2018}} −\mathrm{1}\right)}{{p}−\mathrm{1}}{A}+\frac{{q}\left({q}^{\mathrm{2018}} −\mathrm{1}\right)}{{q}−\mathrm{1}}{B}=\mathrm{1945} \\ $$$$…… \\ $$
Commented by jagoll last updated on 04/Apr/20

$$\mathrm{waw}… \\ $$
