Question Number 57232 by maxmathsup by imad last updated on 31/Mar/19
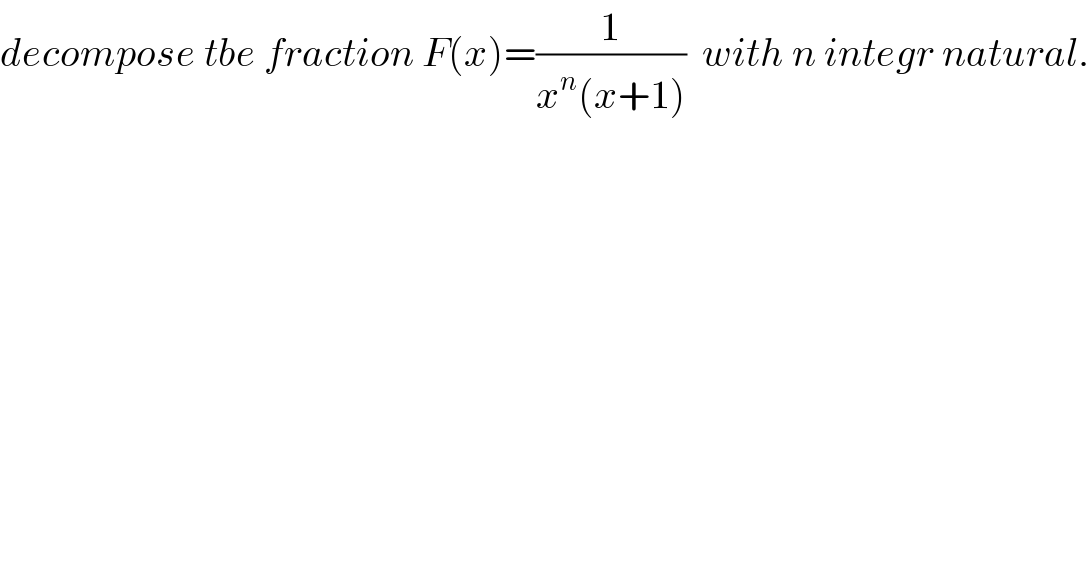
$${decompose}\:{tbe}\:{fraction}\:{F}\left({x}\right)=\frac{\mathrm{1}}{{x}^{{n}} \left({x}+\mathrm{1}\right)}\:\:{with}\:{n}\:{integr}\:{natural}. \\ $$
Commented by maxmathsup by imad last updated on 14/Apr/19
![the dcomposition of F is F(x) =(a/(x+1)) +Σ_(i=1) ^n (λ_i /x^i ) let w(x) =(1/(x+1)) let find D_(n−1) (o)(w) ⇒w(x) =Σ_(k=0) ^(n−1) (x^k /(k!)) w^((k)) (0) +(x^n /(n!)) ξ(x)(ξ(x)→0 f x→0) but w^((k)) (x) =(((−1)^k k!)/((x+1)^(k+1) )) ⇒w^((k)) (0) =(−1)^k k! ⇒w(x) =Σ_(k=0) ^(n−1) (−1)^k x^k +(x^n /(n!))ξ(x) ⇒F(x) =Σ_(k=0) ^(n−1) (((−1)^k )/x^(n−k) ) +(1/(n!))ξ(x) changement of indice n−k =i give F(x) =Σ_(i=1) ^n (((−1)^(n−i) )/x^i ) +(1/(n!))ξ(x) but F(x) =(a/(x+1)) +Σ_(i=1) ^n (λ_i /x^i ) ⇒λ_i =(−1)^(n−i) i∈[[1,n]] we have a =lim_(x→−1) (x+1)F(x) =(−1)^n ⇒ F(x) =(((−1)^n )/(x+1)) +Σ_(i=1) ^n (((−1)^(n−i) )/x^i ) .](https://www.tinkutara.com/question/Q57921.png)
$$\:{the}\:{dcomposition}\:{of}\:{F}\:{is}\:{F}\left({x}\right)\:=\frac{{a}}{{x}+\mathrm{1}}\:+\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\lambda_{{i}} }{{x}^{{i}} }\:\:\:{let}\:{w}\left({x}\right)\:=\frac{\mathrm{1}}{{x}+\mathrm{1}} \\ $$$${let}\:{find}\:\:{D}_{{n}−\mathrm{1}} \left({o}\right)\left({w}\right)\:\Rightarrow{w}\left({x}\right)\:=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{{x}^{{k}} }{{k}!}\:{w}^{\left({k}\right)} \left(\mathrm{0}\right)\:+\frac{{x}^{{n}} }{{n}!}\:\xi\left({x}\right)\left(\xi\left({x}\right)\rightarrow\mathrm{0}\:{f}\:{x}\rightarrow\mathrm{0}\right) \\ $$$${but}\:{w}^{\left({k}\right)} \left({x}\right)\:=\frac{\left(−\mathrm{1}\right)^{{k}} {k}!}{\left({x}+\mathrm{1}\right)^{{k}+\mathrm{1}} }\:\Rightarrow{w}^{\left({k}\right)} \left(\mathrm{0}\right)\:=\left(−\mathrm{1}\right)^{{k}} \:{k}!\:\Rightarrow{w}\left({x}\right)\:=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\left(−\mathrm{1}\right)^{{k}} \:{x}^{{k}} \:+\frac{{x}^{{n}} }{{n}!}\xi\left({x}\right) \\ $$$$\Rightarrow{F}\left({x}\right)\:=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\frac{\left(−\mathrm{1}\right)^{{k}} }{{x}^{{n}−{k}} }\:+\frac{\mathrm{1}}{{n}!}\xi\left({x}\right)\:\:\:\:{changement}\:{of}\:{indice}\:{n}−{k}\:={i}\:{give} \\ $$$${F}\left({x}\right)\:=\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{n}−{i}} }{{x}^{{i}} }\:+\frac{\mathrm{1}}{{n}!}\xi\left({x}\right)\:{but}\:{F}\left({x}\right)\:=\frac{{a}}{{x}+\mathrm{1}}\:+\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\lambda_{{i}} }{{x}^{{i}} }\:\Rightarrow\lambda_{{i}} =\left(−\mathrm{1}\right)^{{n}−{i}} \\ $$$${i}\in\left[\left[\mathrm{1},{n}\right]\right]\:\:\:\:{we}\:{have}\:{a}\:={lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right){F}\left({x}\right)\:=\left(−\mathrm{1}\right)^{{n}} \:\Rightarrow \\ $$$${F}\left({x}\right)\:=\frac{\left(−\mathrm{1}\right)^{{n}} }{{x}+\mathrm{1}}\:+\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{n}−{i}} }{{x}^{{i}} }\:. \\ $$$$ \\ $$
