Define-the-laplace-transformation-equation-and-use-the-transformation-equation-transform-dy-dx-and-d-2-y-dx-2-hence-solve-the-equation-d-2-y-dx-2-5-dy-dx-4-e-x-sin-2x-Using-the-l

FacebookTweetPin

Question Number 110178 by Rio Michael last updated on 27/Aug/20

$$\mathrm{Define}\mathrm{the}\mathrm{laplace}\mathrm{transformation}\mathrm{equation}\mathrm{and}$$$$\mathrm{use}\mathrm{the}\mathrm{transformation}\mathrm{equation}\mathrm{transform}\frac{dy}{dx}\mathrm{and}\frac{d^{2}y}{{dx}^2}$$$$\mathrm{hence}\mathrm{solve}\mathrm{the}\mathrm{equation}:\frac{d^{2}y}{{dx}^2}+5\frac{dy}{dx}+4=e^{-x}\sin 2x$$$$\mathrm{Using}\mathrm{the}\mathrm{laplace}\mathrm{transformation}\mathrm{equations}\mathrm{derived}\mathrm{above}.$$

Answered by Aziztisffola last updated on 27/Aug/20

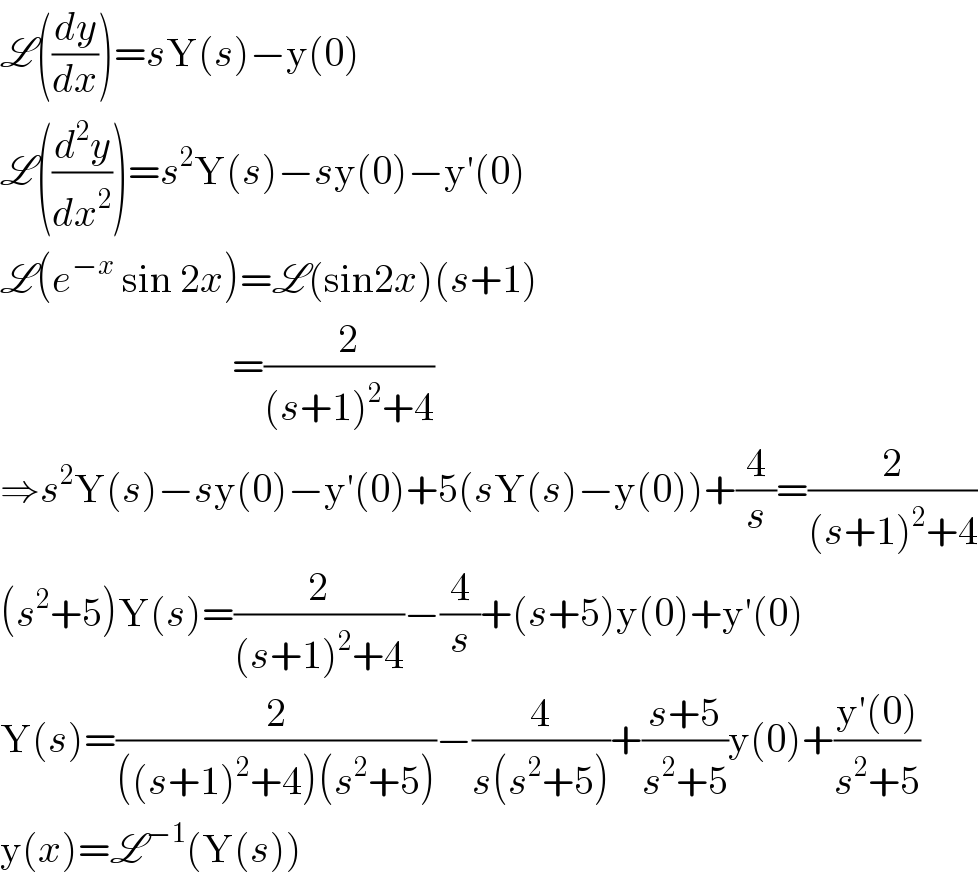
$$\mathcal{L}\left(\frac{dy}{dx}\right)=s\mathrm{Y}\left(s\right)-\mathrm{y}\left(0\right)$$$$\mathcal{L}\left(\frac{d^{2}y}{{dx}^2}\right)=s^2\mathrm{Y}\left(s\right)-s\mathrm{y}\left(0\right)-{\mathrm{y}}^{\prime }\left(0\right)$$$$\mathcal{L}\left(e^{-x}\sin 2x\right)=\mathcal{L}\left(\sin 2x\right)(s+1)$$$$=\frac{2}{{(s+1)}^2+4}$$$$\Rightarrow s^2\mathrm{Y}\left(s\right)-s\mathrm{y}\left(0\right)-{\mathrm{y}}^{\prime }\left(0\right)+5(s\mathrm{Y}\left(s\right)-\mathrm{y}\left(0\right))+\frac{4}{s}=\frac{2}{{(s+1)}^2+4}$$$$(s^2+5)\mathrm{Y}\left(s\right)=\frac{2}{{(s+1)}^2+4}-\frac{4}{s}+(s+5)\mathrm{y}\left(0\right)+{\mathrm{y}}^{\prime }\left(0\right)$$$$\mathrm{Y}\left(s\right)=\frac{2}{({(s+1)}^2+4)(s^2+5)}-\frac{4}{s(s^2+5)}+\frac{s+5}{s^2+5}\mathrm{y}\left(0\right)+\frac{{\mathrm{y}}^{\prime }\left(0\right)}{s^2+5}$$$$\mathrm{y}\left(x\right)={\mathcal{L}}^{-1}\left(\mathrm{Y}\left(s\right)\right)$$

Commented by Rio Michael last updated on 27/Aug/20

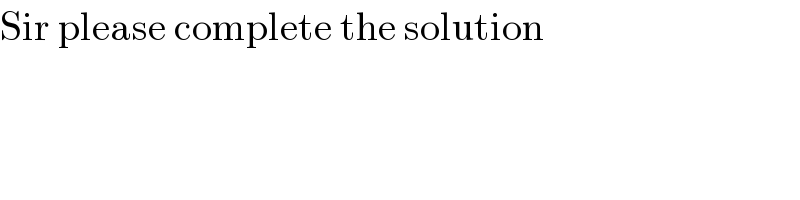
$$\mathrm{Sir}\mathrm{please}\mathrm{complete}\mathrm{the}\mathrm{solution}$$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

FacebookTweetPin