Question Number 183236 by a.lgnaoui last updated on 23/Dec/22
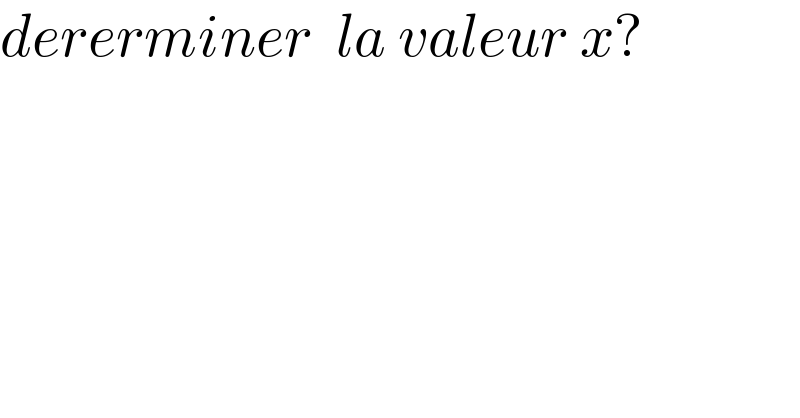
$${dererminer}\:\:{la}\:{valeur}\:{x}? \\ $$
Commented by a.lgnaoui last updated on 23/Dec/22

Commented by mr W last updated on 24/Dec/22

$$“\boldsymbol{{par}}\:\boldsymbol{{mesure}}''\:\boldsymbol{{method}} \\ $$$${x}=\mathrm{9} \\ $$$${how}\:{i}\:{got}? \\ $$$${i}\:{measured}\:{with}\:{a}\:{ruler}. \\ $$
Answered by mr W last updated on 24/Dec/22
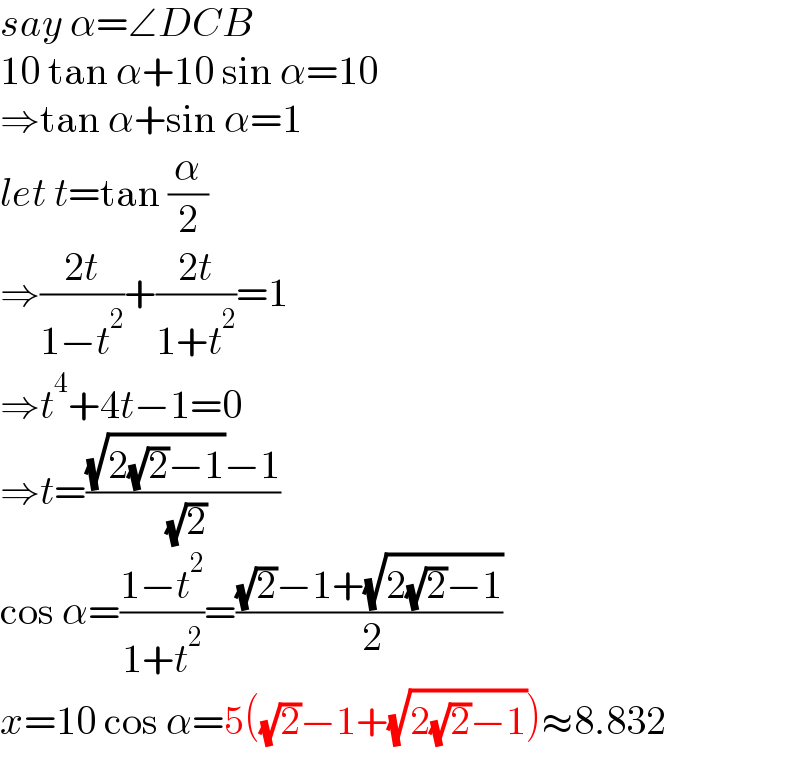
$${say}\:\alpha=\angle{DCB} \\ $$$$\mathrm{10}\:\mathrm{tan}\:\alpha+\mathrm{10}\:\mathrm{sin}\:\alpha=\mathrm{10} \\ $$$$\Rightarrow\mathrm{tan}\:\alpha+\mathrm{sin}\:\alpha=\mathrm{1} \\ $$$${let}\:{t}=\mathrm{tan}\:\frac{\alpha}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow{t}^{\mathrm{4}} +\mathrm{4}{t}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{t}=\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }=\frac{\sqrt{\mathrm{2}}−\mathrm{1}+\sqrt{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}}}{\:\mathrm{2}} \\ $$$${x}=\mathrm{10}\:\mathrm{cos}\:\alpha=\mathrm{5}\left(\sqrt{\mathrm{2}}−\mathrm{1}+\sqrt{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}}\right)\approx\mathrm{8}.\mathrm{832} \\ $$
