Question Number 108349 by Ar Brandon last updated on 16/Aug/20
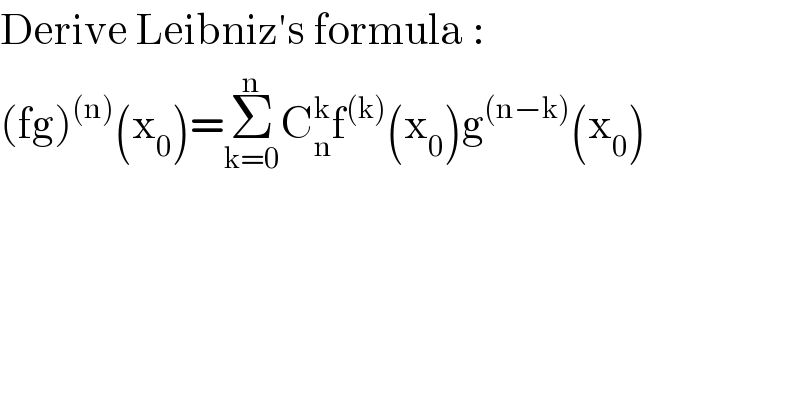
$$\mathrm{Derive}\:\mathrm{Leibniz}'\mathrm{s}\:\mathrm{formula}\:: \\ $$$$\left(\mathrm{fg}\right)^{\left(\mathrm{n}\right)} \left(\mathrm{x}_{\mathrm{0}} \right)=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \mathrm{f}^{\left(\mathrm{k}\right)} \left(\mathrm{x}_{\mathrm{0}} \right)\mathrm{g}^{\left(\mathrm{n}−\mathrm{k}\right)} \left(\mathrm{x}_{\mathrm{0}} \right) \\ $$
