Question Number 169702 by Anyangwa last updated on 06/May/22
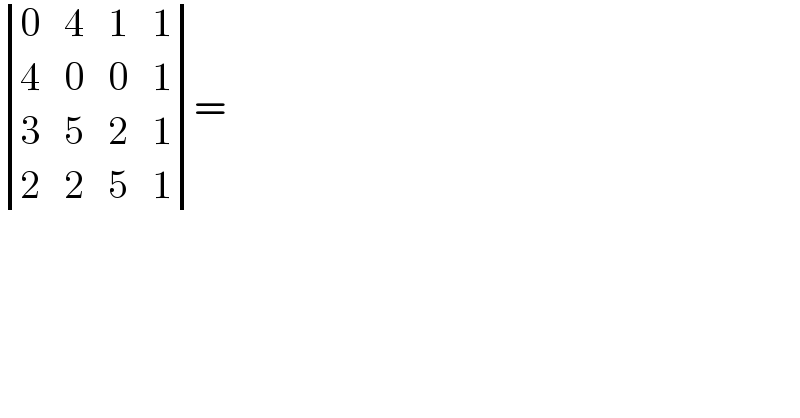
$$\begin{vmatrix}{\mathrm{0}}&{\mathrm{4}}&{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{4}}&{\mathrm{0}}&{\mathrm{0}}&{\mathrm{1}}\\{\mathrm{3}}&{\mathrm{5}}&{\mathrm{2}}&{\mathrm{1}}\\{\mathrm{2}}&{\mathrm{2}}&{\mathrm{5}}&{\mathrm{1}}\end{vmatrix}=\: \\ $$
Answered by MikeH last updated on 06/May/22
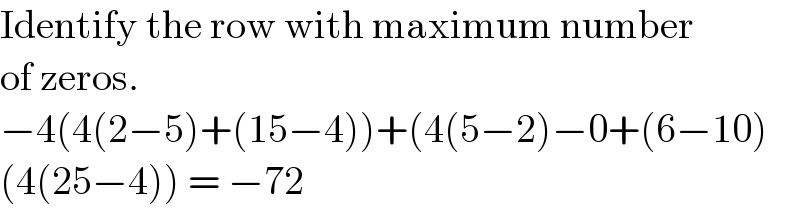
$$\mathrm{Identify}\:\mathrm{the}\:\mathrm{row}\:\mathrm{with}\:\mathrm{maximum}\:\mathrm{number} \\ $$$$\mathrm{of}\:\mathrm{zeros}. \\ $$$$−\mathrm{4}\left(\mathrm{4}\left(\mathrm{2}−\mathrm{5}\right)+\left(\mathrm{15}−\mathrm{4}\right)\right)+\left(\mathrm{4}\left(\mathrm{5}−\mathrm{2}\right)−\mathrm{0}+\left(\mathrm{6}−\mathrm{10}\right)\right. \\ $$$$\left(\mathrm{4}\left(\mathrm{25}−\mathrm{4}\right)\right)\:=\:−\mathrm{72} \\ $$
