Question Number 184010 by Rasheed.Sindhi last updated on 01/Jan/23

$$\:\:\:\:\:\:\:\:\:\:\underset{\:\underset{\underset{\underset{\underset{\underset{\bullet} {\bullet}} {\boldsymbol{\mathrm{by}}}} {\boldsymbol{\mathrm{which}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{divisible}}}} {\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{number}}}} {\boldsymbol{\mathrm{is}}^{\:} }} {\begin{array}{|c|}{\:\begin{array}{|c|}{\mathrm{2023}}\\\hline\end{array}\:}\\\hline\end{array}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\boldsymbol{\mathrm{i}}\right)\boldsymbol{\mathrm{its}}\:\boldsymbol{\mathrm{sum}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{digits}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\& \\ $$$$\:\:\:\:\:\:\:\left(\boldsymbol{\mathrm{ii}}\right)\boldsymbol{\mathrm{its}}\:\boldsymbol{\mathrm{sum}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{squares}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{digits}} \\ $$
Commented by Rasheed.Sindhi last updated on 01/Jan/23
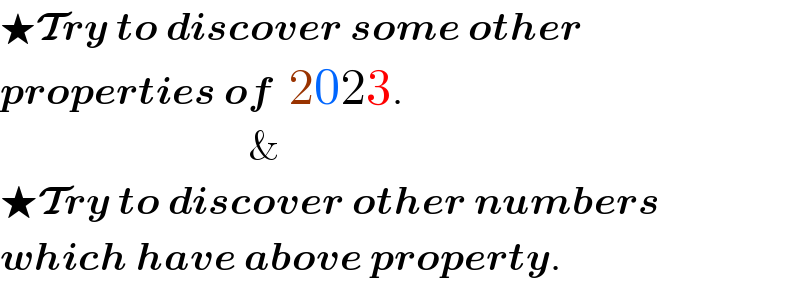
$$\bigstar\boldsymbol{\mathcal{T}{ry}}\:\boldsymbol{{to}}\:\boldsymbol{{discover}}\:\boldsymbol{{some}}\:\boldsymbol{{other}} \\ $$$$\boldsymbol{{properties}}\:\boldsymbol{{of}}\:\:\mathrm{2023}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\& \\ $$$$\bigstar\boldsymbol{\mathcal{T}{ry}}\:\boldsymbol{{to}}\:\boldsymbol{{discover}}\:\boldsymbol{{other}}\:\boldsymbol{{numbers}} \\ $$$$\boldsymbol{{which}}\:\boldsymbol{{have}}\:\boldsymbol{{above}}\:\boldsymbol{{property}}. \\ $$
Commented by nikif99 last updated on 02/Jan/23

$$\mathrm{7}^{\mathrm{7}} \:{mod}\:\mathrm{7}!\:=\:\mathrm{2023}.\:{Happy}\:{new}\:{year}. \\ $$
Commented by Rasheed.Sindhi last updated on 02/Jan/23

$$\bullet\cap\boldsymbol{\mathrm{i}}\subset\in\:\mathrm{property}\:\mathrm{sir}!\:\mathrm{Is}\:\mathrm{it}\:\mathrm{your}\:\mathrm{own} \\ $$$$\mathrm{discovery}? \\ $$$$\bullet\mathrm{HappyNewYear}\:\mathrm{to}\:\mathrm{you}\:\mathrm{too}, \\ $$$$\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{nikif}}! \\ $$
