Question Number 172309 by mathocean1 last updated on 25/Jun/22
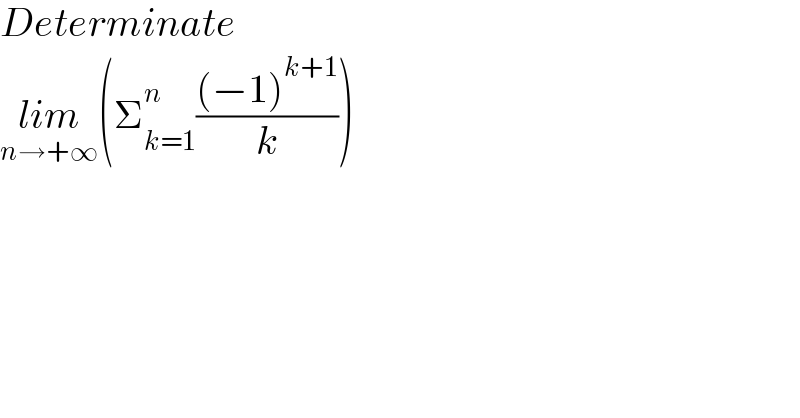
$${Determinate}\: \\ $$$$\underset{{n}\rightarrow+\infty} {{lim}}\left(\sum_{{k}=\mathrm{1}} ^{{n}} \frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} }{{k}}\right) \\ $$
Commented by mr W last updated on 25/Jun/22
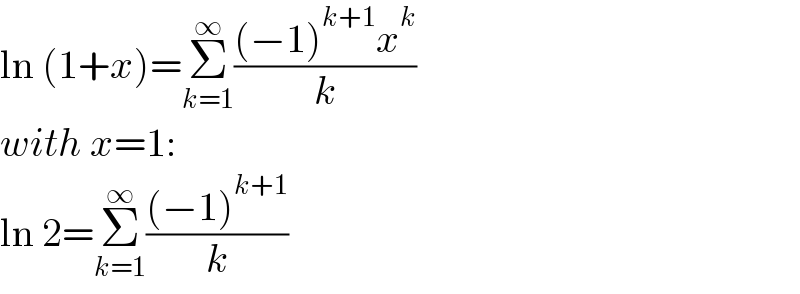
$$\mathrm{ln}\:\left(\mathrm{1}+{x}\right)=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} {x}^{{k}} }{{k}} \\ $$$${with}\:{x}=\mathrm{1}: \\ $$$$\mathrm{ln}\:\mathrm{2}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} }{{k}} \\ $$
Answered by Mathspace last updated on 25/Jun/22
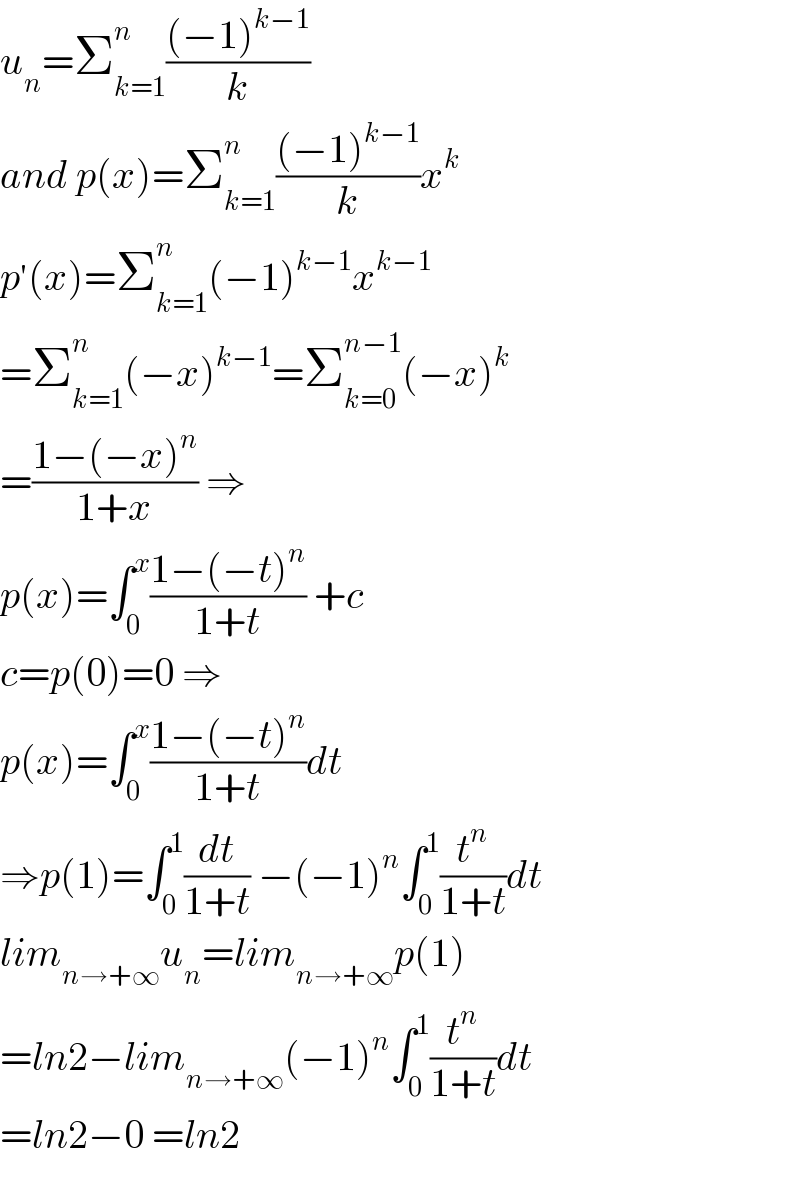
$${u}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} }{{k}} \\ $$$${and}\:{p}\left({x}\right)=\sum_{{k}=\mathrm{1}} ^{{n}} \frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} }{{k}}{x}^{{k}} \\ $$$${p}^{'} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{{n}} \left(−\mathrm{1}\right)^{{k}−\mathrm{1}} {x}^{{k}−\mathrm{1}} \\ $$$$=\sum_{{k}=\mathrm{1}} ^{{n}} \left(−{x}\right)^{{k}−\mathrm{1}} =\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left(−{x}\right)^{{k}} \\ $$$$=\frac{\mathrm{1}−\left(−{x}\right)^{{n}} }{\mathrm{1}+{x}}\:\Rightarrow \\ $$$${p}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \frac{\mathrm{1}−\left(−{t}\right)^{{n}} }{\mathrm{1}+{t}}\:+{c} \\ $$$${c}={p}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow \\ $$$${p}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \frac{\mathrm{1}−\left(−{t}\right)^{{n}} }{\mathrm{1}+{t}}{dt} \\ $$$$\Rightarrow{p}\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\mathrm{1}+{t}}\:−\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{{n}} }{\mathrm{1}+{t}}{dt} \\ $$$${lim}_{{n}\rightarrow+\infty} {u}_{{n}} ={lim}_{{n}\rightarrow+\infty} {p}\left(\mathrm{1}\right) \\ $$$$={ln}\mathrm{2}−{lim}_{{n}\rightarrow+\infty} \left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{{n}} }{\mathrm{1}+{t}}{dt} \\ $$$$={ln}\mathrm{2}−\mathrm{0}\:={ln}\mathrm{2} \\ $$
