Question Number 122648 by mathocean1 last updated on 18/Nov/20
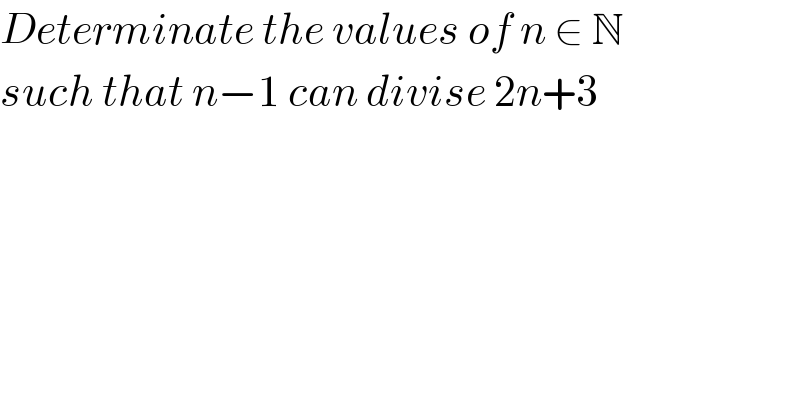
$${Determinate}\:{the}\:{values}\:{of}\:{n}\:\in\:\mathbb{N} \\ $$$${such}\:{that}\:{n}−\mathrm{1}\:{can}\:{divise}\:\mathrm{2}{n}+\mathrm{3} \\ $$
Answered by TANMAY PANACEA last updated on 18/Nov/20

$$\mathrm{2}{n}−\mathrm{2}+\mathrm{5}\:\:\:{when}\:{devided}\:{by}\:{n}−\mathrm{1} \\ $$$$\mathrm{2}+\frac{\mathrm{5}}{{n}−\mathrm{1}}\:\:\:\:\:{n}\:{should}\:{be}\:\mathrm{6} \\ $$
Commented by mathocean1 last updated on 18/Nov/20

$${thank}\:{you}\:{sir} \\ $$
Answered by MJS_new last updated on 18/Nov/20
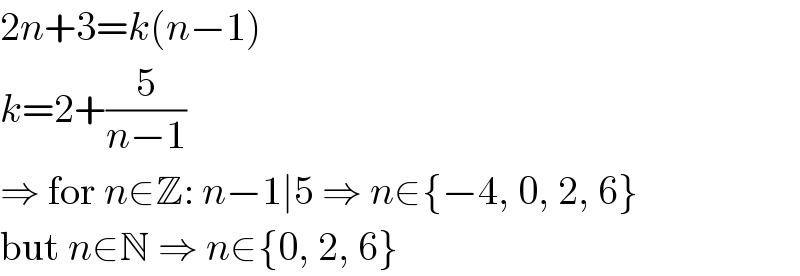
$$\mathrm{2}{n}+\mathrm{3}={k}\left({n}−\mathrm{1}\right) \\ $$$${k}=\mathrm{2}+\frac{\mathrm{5}}{{n}−\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{for}\:{n}\in\mathbb{Z}:\:{n}−\mathrm{1}\mid\mathrm{5}\:\Rightarrow\:{n}\in\left\{−\mathrm{4},\:\mathrm{0},\:\mathrm{2},\:\mathrm{6}\right\} \\ $$$$\mathrm{but}\:{n}\in\mathbb{N}\:\Rightarrow\:{n}\in\left\{\mathrm{0},\:\mathrm{2},\:\mathrm{6}\right\} \\ $$
