Determine-a-cos-sin-1-x-b-sin-cos-1-x-c-cos-1-sin-x-d-sin-1-cos-x-e-sin-1-sin-x-f-sin-sin-1-x-g-sin-1-sin-1-x-h-sin-sin-x-

Question Number 14366 by RasheedSindhi last updated on 31/May/17

$$\mathrm{Determine} \\ $$$$\left.\mathrm{a}\right)\:\mathrm{cos}\left(\mathrm{sin}^{-\mathrm{1}} \mathrm{x}\right) \\ $$$$\left.\mathrm{b}\right)\:\mathrm{sin}\left(\mathrm{cos}^{-\mathrm{1}} \mathrm{x}\right) \\ $$$$\left.\mathrm{c}\right)\:\mathrm{cos}^{-\mathrm{1}} \left(\mathrm{sin}\:\mathrm{x}\right) \\ $$$$\left.\mathrm{d}\right)\:\mathrm{sin}^{-\mathrm{1}} \left(\mathrm{cos}\:\mathrm{x}\right) \\ $$$$\left.\mathrm{e}\right)\:\mathrm{sin}^{-\mathrm{1}} \left(\mathrm{sin}\:\mathrm{x}\right) \\ $$$$\left.\mathrm{f}\right)\:\mathrm{sin}\left(\mathrm{sin}^{-\mathrm{1}} \:\mathrm{x}\right) \\ $$$$\left.\mathrm{g}\right)\:\mathrm{sin}^{-\mathrm{1}} \left(\mathrm{sin}^{-\mathrm{1}} \:\mathrm{x}\right) \\ $$$$\left.\mathrm{h}\right)\:\mathrm{sin}\left(\mathrm{sin}\:\mathrm{x}\right) \\ $$

Commented by Tinkutara last updated on 31/May/17

$$\mathrm{sin}\:\left(\mathrm{sin}^{−\mathrm{1}} \:{x}\right)\:=\:{x}\:\left(\mathrm{Principal}\:\mathrm{value}\:\mathrm{in}\right. \\ $$$$\left.\mathrm{the}\:\mathrm{interval}\:\left[\frac{−\pi}{\mathrm{2}}\:,\:\frac{\pi}{\mathrm{2}}\right]\right) \\ $$

Commented by RasheedSindhi last updated on 01/Jun/17

$$\mathrm{Thank}\:\mathrm{you}. \\ $$

Answered by mrW1 last updated on 31/May/17

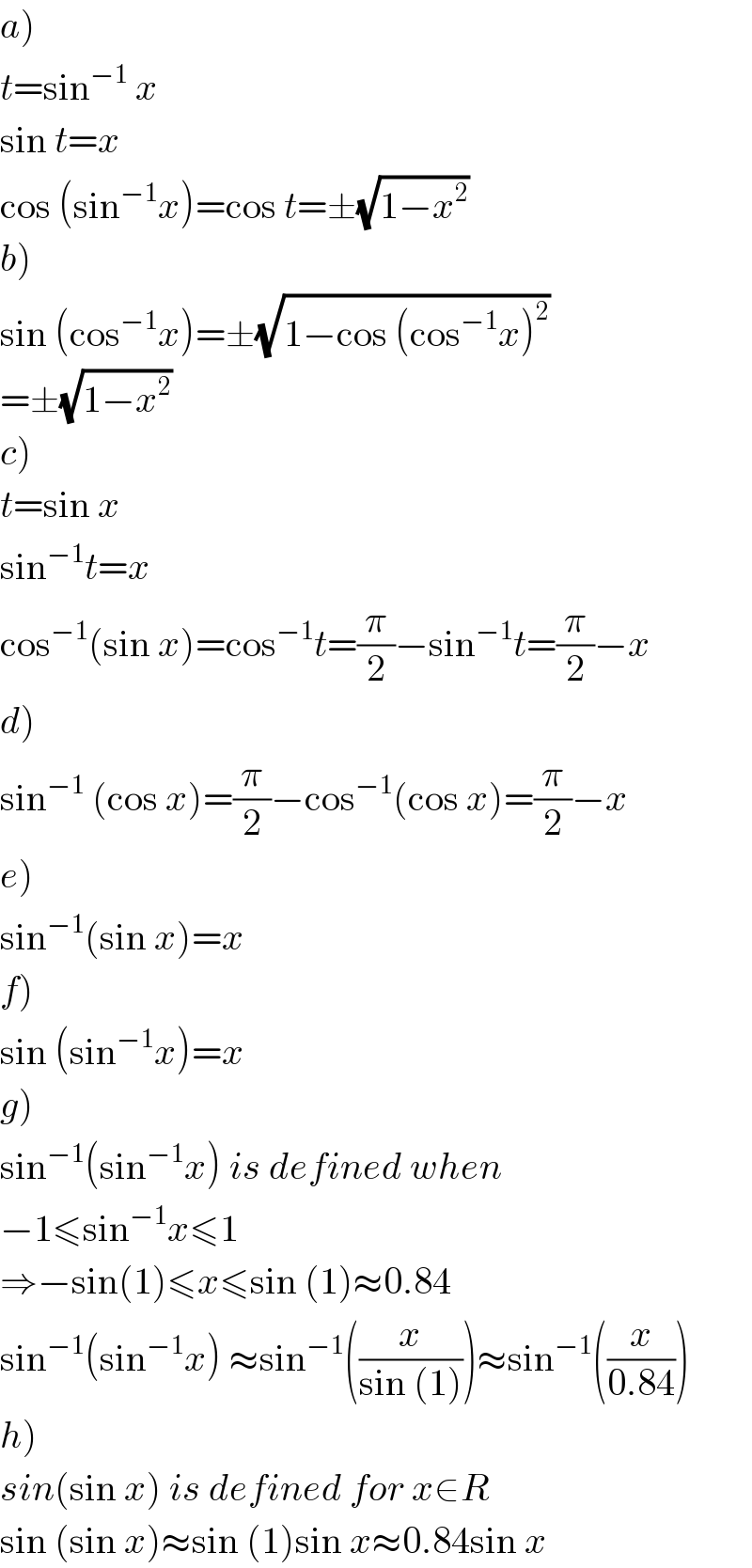
$$\left.{a}\right) \\ $$$${t}=\mathrm{sin}^{−\mathrm{1}} \:{x} \\ $$$$\mathrm{sin}\:{t}={x} \\ $$$$\mathrm{cos}\:\left(\mathrm{sin}^{−\mathrm{1}} {x}\right)=\mathrm{cos}\:{t}=\pm\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\left.{b}\right) \\ $$$$\mathrm{sin}\:\left(\mathrm{cos}^{−\mathrm{1}} {x}\right)=\pm\sqrt{\mathrm{1}−\mathrm{cos}\:\left(\mathrm{cos}^{−\mathrm{1}} {x}\right)^{\mathrm{2}} } \\ $$$$=\pm\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\left.{c}\right) \\ $$$${t}=\mathrm{sin}\:{x} \\ $$$$\mathrm{sin}^{−\mathrm{1}} {t}={x} \\ $$$$\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{sin}\:{x}\right)=\mathrm{cos}^{−\mathrm{1}} {t}=\frac{\pi}{\mathrm{2}}−\mathrm{sin}^{−\mathrm{1}} {t}=\frac{\pi}{\mathrm{2}}−{x} \\ $$$$\left.{d}\right) \\ $$$$\mathrm{sin}^{−\mathrm{1}} \:\left(\mathrm{cos}\:{x}\right)=\frac{\pi}{\mathrm{2}}−\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{cos}\:{x}\right)=\frac{\pi}{\mathrm{2}}−{x} \\ $$$$\left.{e}\right) \\ $$$$\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\:{x}\right)={x} \\ $$$$\left.{f}\right) \\ $$$$\mathrm{sin}\:\left(\mathrm{sin}^{−\mathrm{1}} {x}\right)={x} \\ $$$$\left.{g}\right) \\ $$$$\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}^{−\mathrm{1}} {x}\right)\:{is}\:{defined}\:{when} \\ $$$$−\mathrm{1}\leqslant\mathrm{sin}^{−\mathrm{1}} {x}\leqslant\mathrm{1} \\ $$$$\Rightarrow−\mathrm{sin}\left(\mathrm{1}\right)\leqslant{x}\leqslant\mathrm{sin}\:\left(\mathrm{1}\right)\approx\mathrm{0}.\mathrm{84} \\ $$$$\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}^{−\mathrm{1}} {x}\right)\:\approx\mathrm{sin}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{sin}\:\left(\mathrm{1}\right)}\right)\approx\mathrm{sin}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{0}.\mathrm{84}}\right) \\ $$$$\left.{h}\right) \\ $$$${sin}\left(\mathrm{sin}\:{x}\right)\:{is}\:{defined}\:{for}\:{x}\in{R} \\ $$$$\mathrm{sin}\:\left(\mathrm{sin}\:{x}\right)\approx\mathrm{sin}\:\left(\mathrm{1}\right)\mathrm{sin}\:{x}\approx\mathrm{0}.\mathrm{84sin}\:{x} \\ $$

Commented by RasheedSindhi last updated on 01/Jun/17

$$\mathcal{T}\mathrm{h}{a}\mathrm{n}{k}\mathrm{s}\:\mathrm{Sir}! \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com