Question Number 118150 by bobhans last updated on 15/Oct/20
$$\mathrm{Determine}\:\mathrm{all}\:\mathrm{function}\:\mathrm{f}:\mathbb{R}\diagdown\left\{\mathrm{0},\mathrm{1}\right\}\:\rightarrow\mathbb{R} \\ $$$$\mathrm{satisfying}\:\mathrm{the}\:\mathrm{functional}\:\mathrm{relation} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)\:=\:\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{2x}\right)}{\mathrm{x}\left(\mathrm{1}−\mathrm{x}\right)};\:\mathrm{for}\:\mathrm{x}\neq\mathrm{0}\:\mathrm{and}\:\mathrm{x}\neq\mathrm{1} \\ $$
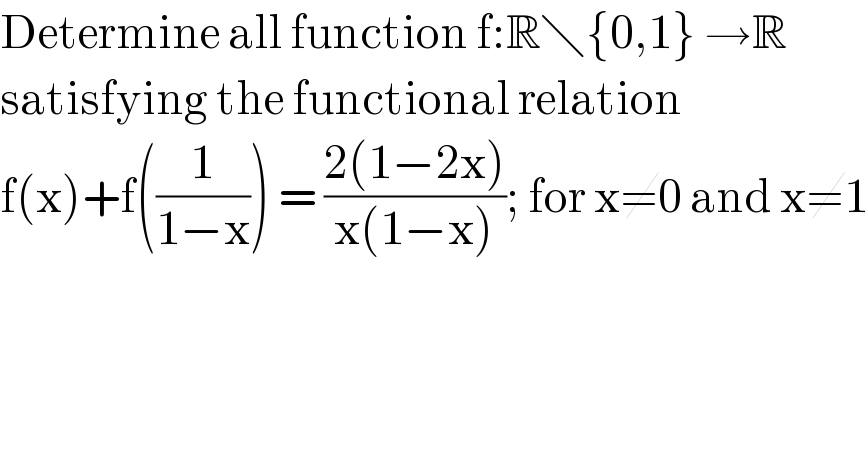
Commented by bemath last updated on 15/Oct/20
$${good}\:{question} \\ $$
Answered by bemath last updated on 15/Oct/20
$${letting}\:{w}\:=\:\frac{\mathrm{1}}{\mathrm{1}−{x}},\:{the}\:{given}\:{functional} \\ $$$${equation}\:{can}\:{be}\:{written}\:{as}\: \\ $$$${f}\left({x}\right)+{f}\left({w}\right)\:=\:\mathrm{2}\left(\frac{\mathrm{1}}{{x}}−{w}\right)…\left({i}\right) \\ $$$${If}\:{we}\:{setting}\:{z}=\frac{\mathrm{1}}{\mathrm{1}−{w}}\:{then}\:{x}=\frac{\mathrm{1}}{\mathrm{1}−{z}} \\ $$$${Hence}\:{we}\:{also}\:{have}\:{the}\:{relation} \\ $$$${f}\left({w}\right)+{f}\left({z}\right)\:=\:\mathrm{2}\left(\frac{\mathrm{1}}{{w}}−{z}\right)…\left({ii}\right) \\ $$$${and}\:{f}\left({z}\right)+{f}\left({x}\right)=\mathrm{2}\left(\frac{\mathrm{1}}{{z}}−{x}\right)…\left({iii}\right) \\ $$$${adding}\:\left({i}\right){and}\:\left({iii}\right)\:{we}\:{get} \\ $$$$\mathrm{2}\left\{{f}\left({x}\right)+{f}\left({w}\right)+{f}\left({z}\right)\right\}=\mathrm{2}\left(\frac{\mathrm{1}}{{x}}−{x}\right)−\mathrm{2}{w}+\frac{\mathrm{2}}{{x}} \\ $$$${using}\:\left({ii}\right)\:{relation},\:{this}\:{reduces} \\ $$$${to}\Rightarrow\:\mathrm{2}{f}\left({x}\right)=\mathrm{2}\left(\frac{\mathrm{1}}{{x}}−{x}\right)−\mathrm{2}\left({w}+\frac{\mathrm{1}}{{w}}\right)+\mathrm{2}\left({z}+\frac{\mathrm{1}}{{z}}\right) \\ $$$${now}\:{using}\:{w}+\frac{\mathrm{1}}{{w}}=\frac{\mathrm{1}}{\mathrm{1}−{x}}+\mathrm{1}−{x} \\ $$$${z}+\frac{\mathrm{1}}{{z}}=\frac{{x}−\mathrm{1}}{{x}}+\frac{{x}}{{x}−\mathrm{1}} \\ $$$${thus}\:{we}\:{get}\:{f}\left({x}\right)\:=\:\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}} \\ $$
Answered by bobhans last updated on 15/Oct/20
![(1)replacing (1/(1−x)) by x , gives f(((x−1)/x))+f(x) = ((2(1−2(((x−1)/x))))/((((x−1)/x))(1−(((x−1)/x))))) f(((x−1)/x))+f(x)=((2x(2−x))/((x−1))) (2)replacing x by (1/(1−x)) f((1/(1−x)))+f((1/(1−((1/(1−x))))))=((2(1−2((1/(1−x)))))/(((1/(1−x)))(1−((1/(1−x)))))) f((1/(1−x)))+f(((x−1)/x))=((2(1−x)(1+x))/x) now we have (1)f(x)+f((1/(1−x))) = ((2−4x)/(x−x^2 )) (2)f(((x−1)/x))+f(x)=((4x−2x^2 )/(x−1)) (3)f((1/(1−x)))+f(((x−1)/x))=((2−2x^2 )/x) adding(1),(2)and(3) we get 2[ f(x)+f((1/(1−x)))+f(((x−1)/x)) ]= ((−4x^3 +6x^2 +6x−4)/(x^2 −x)) or f(x)+f((1/(1−x)))+f(((x−1)/x))=((−2x^3 +3x^2 +3x−2)/(x^2 −x)) substitute third equation , gives f(x) = ((−2x^3 +3x^2 +3x−2)/(x^2 −x))−((2−2x^2 )/x) f(x)= ((−2x^3 +3x^2 +3x−2−(2x−2−2x^3 +2x^2 ))/(x^2 −x)) f(x) = ((x^2 +x)/(x^2 −x)) = ((x+1)/(x−1)).](https://www.tinkutara.com/question/Q118159.png)
$$\left(\mathrm{1}\right)\mathrm{replacing}\:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\:\mathrm{by}\:\mathrm{x}\:,\:\mathrm{gives}\: \\ $$$$\mathrm{f}\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}\right)+\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}\right)\right)}{\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}\right)\left(\mathrm{1}−\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}\right)\right)} \\ $$$$\mathrm{f}\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}\right)+\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{2x}\left(\mathrm{2}−\mathrm{x}\right)}{\left(\mathrm{x}−\mathrm{1}\right)} \\ $$$$\left(\mathrm{2}\right)\mathrm{replacing}\:\mathrm{x}\:\mathrm{by}\:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}} \\ $$$$\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)+\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)}\right)=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)\right)}{\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)\left(\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)\right)} \\ $$$$\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)+\mathrm{f}\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}\right)=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{x}\right)\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have}\: \\ $$$$\left(\mathrm{1}\right)\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)\:=\:\frac{\mathrm{2}−\mathrm{4x}}{\mathrm{x}−\mathrm{x}^{\mathrm{2}} } \\ $$$$\left(\mathrm{2}\right)\mathrm{f}\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}\right)+\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{4x}−\mathrm{2x}^{\mathrm{2}} }{\mathrm{x}−\mathrm{1}} \\ $$$$\left(\mathrm{3}\right)\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)+\mathrm{f}\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}\right)=\frac{\mathrm{2}−\mathrm{2x}^{\mathrm{2}} }{\mathrm{x}} \\ $$$$\mathrm{adding}\left(\mathrm{1}\right),\left(\mathrm{2}\right)\mathrm{and}\left(\mathrm{3}\right)\:\mathrm{we}\:\mathrm{get}\: \\ $$$$\mathrm{2}\left[\:\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)+\mathrm{f}\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}\right)\:\right]=\:\frac{−\mathrm{4x}^{\mathrm{3}} +\mathrm{6x}^{\mathrm{2}} +\mathrm{6x}−\mathrm{4}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}} \\ $$$$\mathrm{or}\:\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)+\mathrm{f}\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}\right)=\frac{−\mathrm{2x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} +\mathrm{3x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}} \\ $$$$\mathrm{substitute}\:\mathrm{third}\:\mathrm{equation}\:,\:\mathrm{gives} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{−\mathrm{2x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} +\mathrm{3x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}−\frac{\mathrm{2}−\mathrm{2x}^{\mathrm{2}} }{\mathrm{x}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\:\frac{−\mathrm{2x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} +\mathrm{3x}−\mathrm{2}−\left(\mathrm{2x}−\mathrm{2}−\mathrm{2x}^{\mathrm{3}} +\mathrm{2x}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}\:=\:\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}. \\ $$
Commented by bemath last updated on 15/Oct/20
$${waw}….{great}… \\ $$