Question Number 153763 by mathdanisur last updated on 10/Sep/21
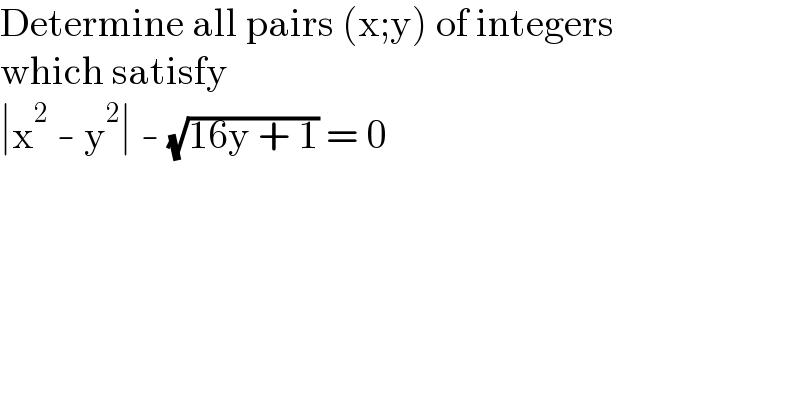
$$\mathrm{Determine}\:\mathrm{all}\:\mathrm{pairs}\:\left(\mathrm{x};\mathrm{y}\right)\:\mathrm{of}\:\mathrm{integers} \\ $$$$\mathrm{which}\:\mathrm{satisfy} \\ $$$$\mid\mathrm{x}^{\mathrm{2}} \:-\:\mathrm{y}^{\mathrm{2}} \mid\:-\:\sqrt{\mathrm{16y}\:+\:\mathrm{1}}\:=\:\mathrm{0} \\ $$
Answered by liberty last updated on 10/Sep/21
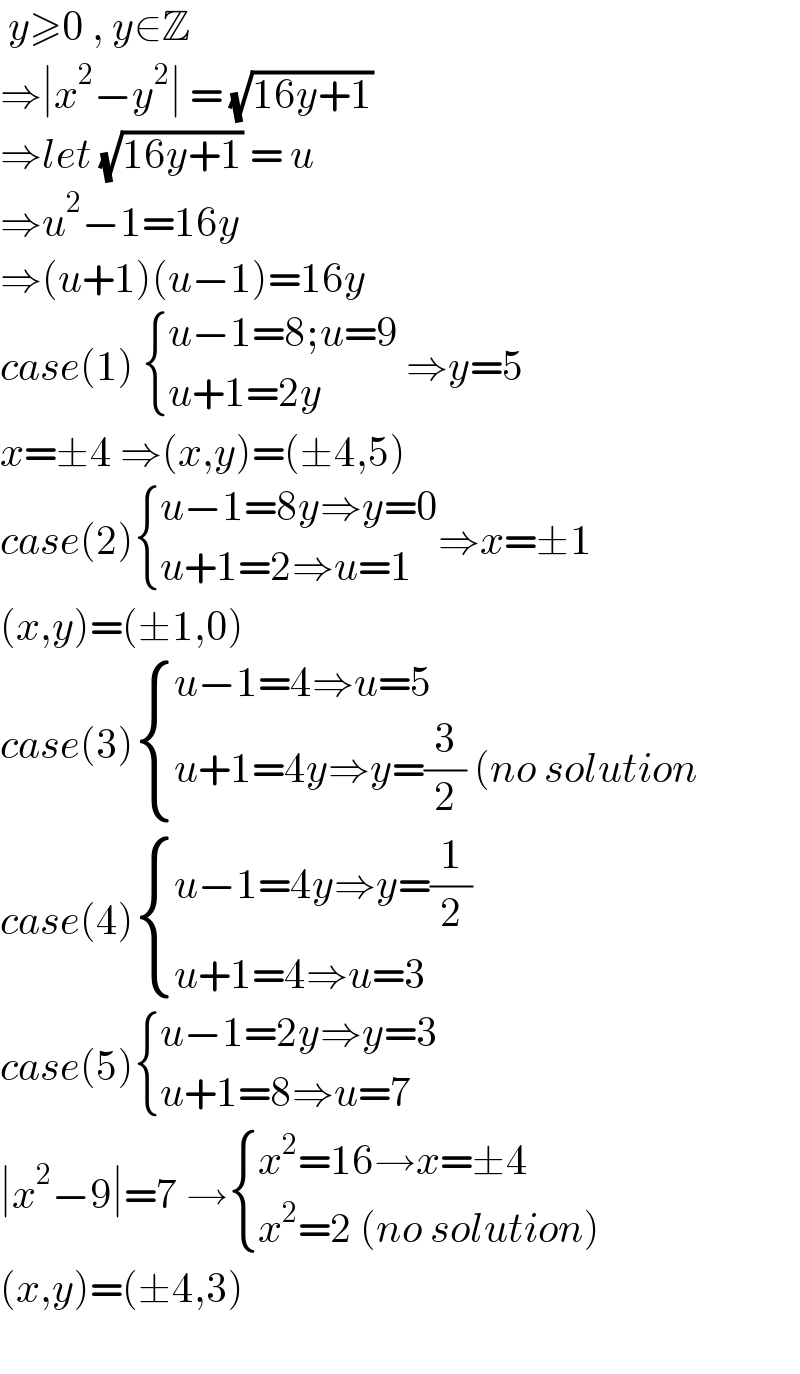
$$\:{y}\geqslant\mathrm{0}\:,\:{y}\in\mathbb{Z} \\ $$$$\Rightarrow\mid{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \mid\:=\:\sqrt{\mathrm{16}{y}+\mathrm{1}} \\ $$$$\Rightarrow{let}\:\sqrt{\mathrm{16}{y}+\mathrm{1}}\:=\:{u} \\ $$$$\Rightarrow{u}^{\mathrm{2}} −\mathrm{1}=\mathrm{16}{y} \\ $$$$\Rightarrow\left({u}+\mathrm{1}\right)\left({u}−\mathrm{1}\right)=\mathrm{16}{y} \\ $$$${case}\left(\mathrm{1}\right)\:\begin{cases}{{u}−\mathrm{1}=\mathrm{8};{u}=\mathrm{9}}\\{{u}+\mathrm{1}=\mathrm{2}{y}}\end{cases}\:\Rightarrow{y}=\mathrm{5} \\ $$$${x}=\pm\mathrm{4}\:\Rightarrow\left({x},{y}\right)=\left(\pm\mathrm{4},\mathrm{5}\right) \\ $$$${case}\left(\mathrm{2}\right)\begin{cases}{{u}−\mathrm{1}=\mathrm{8}{y}\Rightarrow{y}=\mathrm{0}}\\{{u}+\mathrm{1}=\mathrm{2}\Rightarrow{u}=\mathrm{1}}\end{cases}\Rightarrow{x}=\pm\mathrm{1} \\ $$$$\left({x},{y}\right)=\left(\pm\mathrm{1},\mathrm{0}\right) \\ $$$${case}\left(\mathrm{3}\right)\begin{cases}{{u}−\mathrm{1}=\mathrm{4}\Rightarrow{u}=\mathrm{5}}\\{{u}+\mathrm{1}=\mathrm{4}{y}\Rightarrow{y}=\frac{\mathrm{3}}{\mathrm{2}}\:\left({no}\:{solution}\right.}\end{cases}\: \\ $$$${case}\left(\mathrm{4}\right)\begin{cases}{{u}−\mathrm{1}=\mathrm{4}{y}\Rightarrow{y}=\frac{\mathrm{1}}{\mathrm{2}}}\\{{u}+\mathrm{1}=\mathrm{4}\Rightarrow{u}=\mathrm{3}}\end{cases} \\ $$$${case}\left(\mathrm{5}\right)\begin{cases}{{u}−\mathrm{1}=\mathrm{2}{y}\Rightarrow{y}=\mathrm{3}}\\{{u}+\mathrm{1}=\mathrm{8}\Rightarrow{u}=\mathrm{7}}\end{cases} \\ $$$$\mid{x}^{\mathrm{2}} −\mathrm{9}\mid=\mathrm{7}\:\rightarrow\begin{cases}{{x}^{\mathrm{2}} =\mathrm{16}\rightarrow{x}=\pm\mathrm{4}}\\{{x}^{\mathrm{2}} =\mathrm{2}\:\left({no}\:{solution}\right)}\end{cases} \\ $$$$\left({x},{y}\right)=\left(\pm\mathrm{4},\mathrm{3}\right) \\ $$$$ \\ $$
