Question Number 52349 by Tawa1 last updated on 06/Jan/19
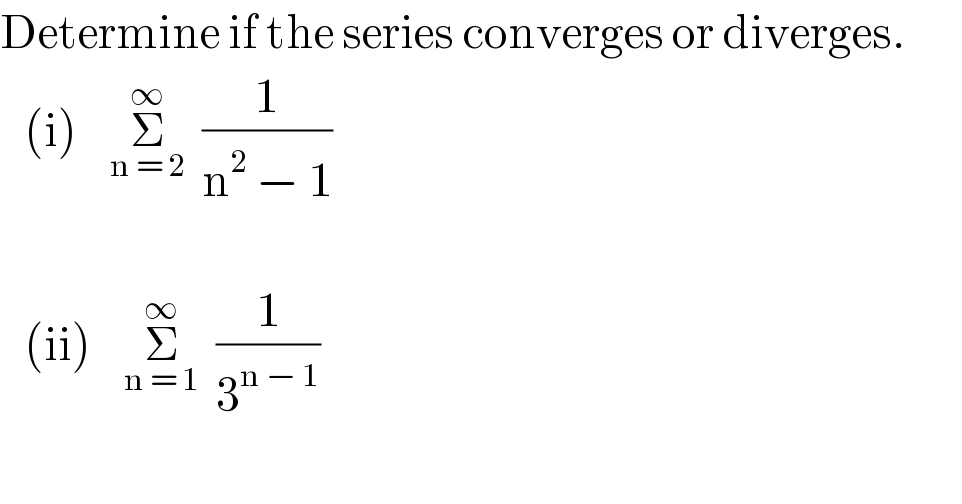
$$\mathrm{Determine}\:\mathrm{if}\:\mathrm{the}\:\mathrm{series}\:\mathrm{converges}\:\mathrm{or}\:\mathrm{diverges}. \\ $$$$\:\:\:\left(\mathrm{i}\right)\:\:\:\:\underset{\mathrm{n}\:=\:\mathrm{2}} {\overset{\infty} {\sum}}\:\:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} \:−\:\mathrm{1}} \\ $$$$ \\ $$$$\:\:\:\left(\mathrm{ii}\right)\:\:\:\:\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\:\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{n}\:−\:\mathrm{1}} } \\ $$$$\:\:\: \\ $$
Commented by Abdo msup. last updated on 07/Jan/19
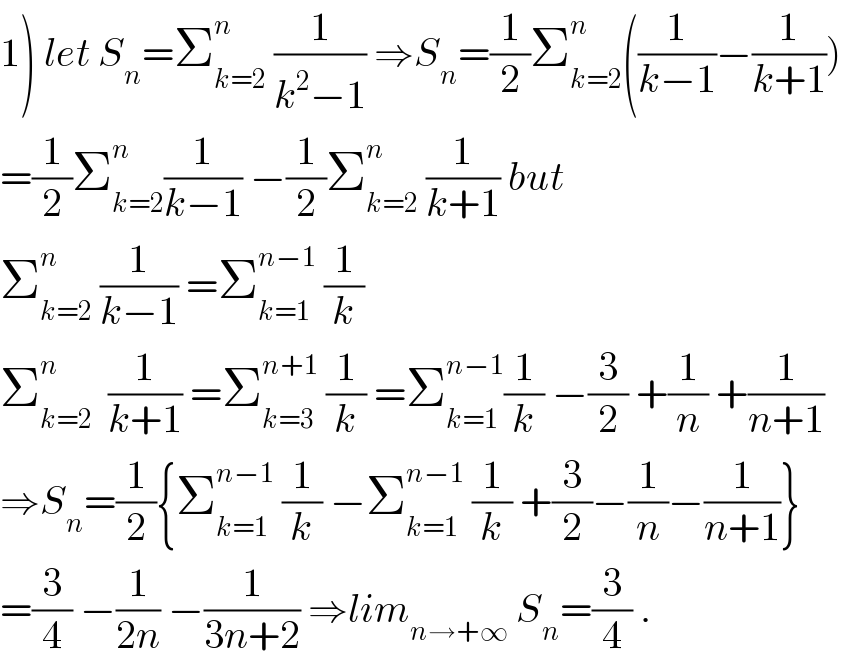
$$\left.\mathrm{1}\right)\:{let}\:{S}_{{n}} =\sum_{{k}=\mathrm{2}} ^{{n}} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} −\mathrm{1}}\:\Rightarrow{S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{2}} ^{{n}} \left(\frac{\mathrm{1}}{{k}−\mathrm{1}}−\frac{\mathrm{1}}{{k}+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{2}} ^{{n}} \frac{\mathrm{1}}{{k}−\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{2}} ^{{n}} \:\frac{\mathrm{1}}{{k}+\mathrm{1}}\:{but} \\ $$$$\sum_{{k}=\mathrm{2}} ^{{n}} \:\frac{\mathrm{1}}{{k}−\mathrm{1}}\:=\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\frac{\mathrm{1}}{{k}} \\ $$$$\sum_{{k}=\mathrm{2}} ^{{n}} \:\:\frac{\mathrm{1}}{{k}+\mathrm{1}}\:=\sum_{{k}=\mathrm{3}} ^{{n}+\mathrm{1}} \:\frac{\mathrm{1}}{{k}}\:=\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \frac{\mathrm{1}}{{k}}\:−\frac{\mathrm{3}}{\mathrm{2}}\:+\frac{\mathrm{1}}{{n}}\:+\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$\Rightarrow{S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\frac{\mathrm{1}}{{k}}\:−\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\frac{\mathrm{1}}{{k}}\:+\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right\} \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\:−\frac{\mathrm{1}}{\mathrm{2}{n}}\:−\frac{\mathrm{1}}{\mathrm{3}{n}+\mathrm{2}}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} =\frac{\mathrm{3}}{\mathrm{4}}\:. \\ $$
Commented by Abdo msup. last updated on 07/Jan/19
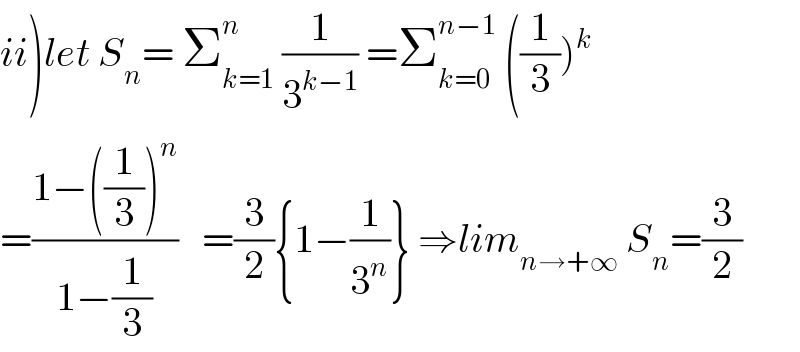
$$\left.{ii}\right){let}\:{S}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{3}^{{k}−\mathrm{1}} }\:=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{k}} \\ $$$$=\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{n}} }{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}}\:\:\:=\frac{\mathrm{3}}{\mathrm{2}}\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}^{{n}} }\right\}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} =\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by Tawa1 last updated on 07/Jan/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Jan/19
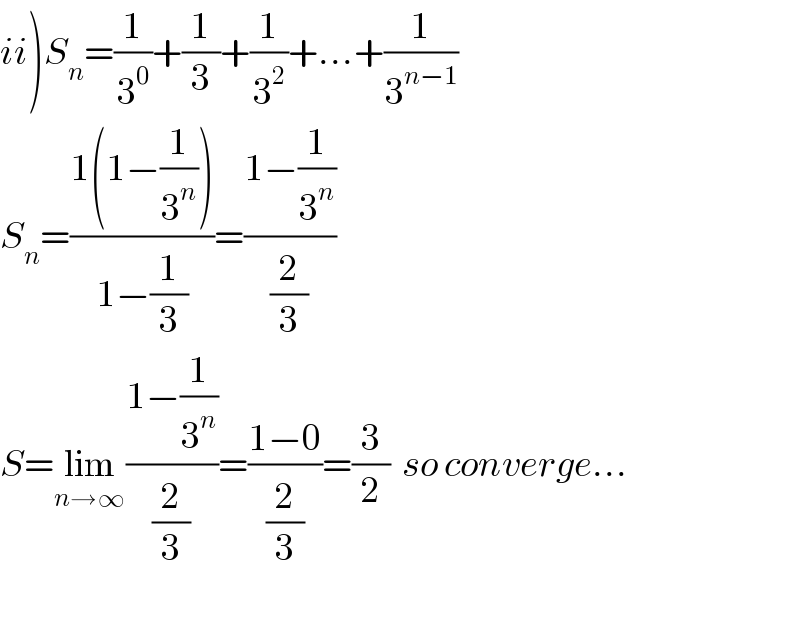
$$\left.{ii}\right){S}_{{n}} =\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{0}} }+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+…+\frac{\mathrm{1}}{\mathrm{3}^{{n}−\mathrm{1}} } \\ $$$${S}_{{n}} =\frac{\mathrm{1}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}^{{n}} }\right)}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}}=\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}^{{n}} }}{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$${S}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}^{{n}} }}{\frac{\mathrm{2}}{\mathrm{3}}}=\frac{\mathrm{1}−\mathrm{0}}{\frac{\mathrm{2}}{\mathrm{3}}}=\frac{\mathrm{3}}{\mathrm{2}}\:\:{so}\:{converge}… \\ $$$$ \\ $$
Commented by Tawa1 last updated on 06/Jan/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Jan/19
![1)T_n =(1/2)[(((n+1)−(n−1))/((n+1)(n−1)))] T_n =(1/2)[(1/(n−1))−(1/(n+1))] T_2 =(1/2)[(1/1)−(1/3)] T_3 =(1/2)[(1/2)−(1/4)] T_4 =(1/2)[(1/3)−(1/5)] T_5 =(1/2)[(1/4)−(1/6)] ... .... now look when we add T_2 +T_3 +T_4 +... all numer cancelled except (1/1) and(1/2) so answdr is=(1/2)[1+(1/2)]=(3/4) so converge...](https://www.tinkutara.com/question/Q52355.png)
$$\left.\mathrm{1}\right){T}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\left({n}+\mathrm{1}\right)−\left({n}−\mathrm{1}\right)}{\left({n}+\mathrm{1}\right)\left({n}−\mathrm{1}\right)}\right] \\ $$$${T}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{{n}−\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right] \\ $$$${T}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}\right] \\ $$$${T}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\right] \\ $$$${T}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}\right] \\ $$$${T}_{\mathrm{5}} =\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{6}}\right] \\ $$$$… \\ $$$$….\:\:{now}\:{look}\:{when}\:{we}\:{add}\:{T}_{\mathrm{2}} +{T}_{\mathrm{3}} +{T}_{\mathrm{4}} +… \\ $$$${all}\:{numer}\:{cancelled}\:{except}\:\frac{\mathrm{1}}{\mathrm{1}}\:{and}\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${so}\:{answdr}\:{is}=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right]=\frac{\mathrm{3}}{\mathrm{4}}\:{so}\:{converge}… \\ $$
Commented by Tawa1 last updated on 06/Jan/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
