Question Number 99460 by mathmax by abdo last updated on 21/Jun/20
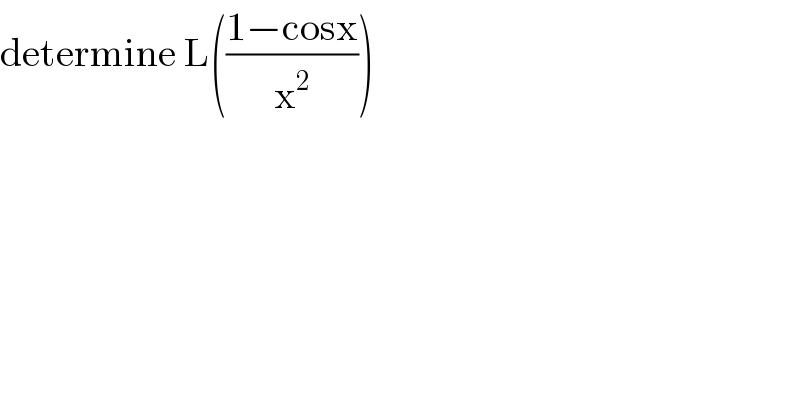
$$\mathrm{determine}\:\mathrm{L}\left(\frac{\mathrm{1}−\mathrm{cosx}}{\mathrm{x}^{\mathrm{2}} }\right) \\ $$
Answered by mathmax by abdo last updated on 23/Jun/20
![L(((1−cosx)/x^2 )) =∫_0 ^∞ ((1−cost)/t^2 )e^(−xt) dt =f(x) ⇒ f^′ (x) =−∫_0 ^∞ (((1−cost)e^(−xt) )/t)dt ⇒f^((2)) (x) =∫_0 ^∞ (1−cost)e^(−xt) dt =∫_0 ^∞ e^(−xt) dt −∫_0 ^∞ e^(−xt) cost dt but ∫_0 ^∞ e^(−xt) dt =[−(1/x)e^(−xt) ]_0 ^∞ =(1/x) and ∫_0 ^∞ e^(−xt) cost dt =Re(∫_0 ^∞ e^(−xt+it) dt) =Re(∫_0 ^∞ e^((−x+i)t) dt) ∫_0 ^∞ e^((−x+i)t) dt =[(1/(−x+i))e^((−x+i)t) ]_0 ^∞ =−(1/(−x+i)) =(1/(x−i)) =((x+i)/(x^2 +1)) ⇒ Re(...) =(x/(x^2 +1)) ⇒f^((2)) (x) =(1/x)−(x/(x^2 +1)) ⇒ f^′ (x) =lnx −(1/2)ln(x^2 +1) +k ⇒ f(x) =∫ ln(x)dx −(1/2)∫ ln(x^2 +1)dx+kx +c we have ∫ ln(x)dx =xln(x)−x ∫ ln(x^2 +1)dx =xln(x^2 +1)−∫ x×((2x)/(1+x^2 ))dx =xln(x^2 +1)−2 ∫ ((x^2 +1−1)/(1+x^2 ))dx =xln(1+x^2 )−2x +2arctanx ⇒ f(x) =xlnx−x−(x/2)ln(1+x^2 )+x −arctanx +kx +c c =lim_(x→0) f(x) =∫_0 ^∞ ((1−cost)/t^2 ) =2 ∫_0 ^∞ ((sin^2 t)/t^2 )dt =2{ [−((sin^2 t)/t)]_0 ^∞ +∫_0 ^∞ ((2sintcost)/t) dt} =2 ∫_0 ^∞ ((sin(2t))/t) dt =_(2t=u) 2∫_0 ^∞ ((sinu)/(u/2))×(du/2) =2∫_0 ^∞ ((sinu)/u)du =π ⇒c =π rest to find k ....be continued....](https://www.tinkutara.com/question/Q99794.png)
$$\mathrm{L}\left(\frac{\mathrm{1}−\mathrm{cosx}}{\mathrm{x}^{\mathrm{2}} }\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}−\mathrm{cost}}{\mathrm{t}^{\mathrm{2}} }\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt}\:\:=\mathrm{f}\left(\mathrm{x}\right)\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{x}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{1}−\mathrm{cost}\right)\mathrm{e}^{−\mathrm{xt}} }{\mathrm{t}}\mathrm{dt}\:\Rightarrow\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\left(\mathrm{1}−\mathrm{cost}\right)\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt}\:−\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{xt}} \:\mathrm{cost}\:\mathrm{dt}\:\:\mathrm{but}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt}\:=\left[−\frac{\mathrm{1}}{\mathrm{x}}\mathrm{e}^{−\mathrm{xt}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}}\:\:\mathrm{and}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{xt}} \:\mathrm{cost}\:\mathrm{dt}\:=\mathrm{Re}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{xt}+\mathrm{it}} \mathrm{dt}\right)\:=\mathrm{Re}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{i}\right)\mathrm{t}} \mathrm{dt}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{i}\right)\mathrm{t}} \:\mathrm{dt}\:=\left[\frac{\mathrm{1}}{−\mathrm{x}+\mathrm{i}}\mathrm{e}^{\left(−\mathrm{x}+\mathrm{i}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \:=−\frac{\mathrm{1}}{−\mathrm{x}+\mathrm{i}}\:=\frac{\mathrm{1}}{\mathrm{x}−\mathrm{i}}\:=\frac{\mathrm{x}+\mathrm{i}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{Re}\left(…\right)\:=\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{x}\right)\:=\mathrm{lnx}\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)\:+\mathrm{k}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\int\:\mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx}\:−\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{dx}+\mathrm{kx}\:+\mathrm{c}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int\:\mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx}\:=\mathrm{xln}\left(\mathrm{x}\right)−\mathrm{x} \\ $$$$\int\:\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{dx}\:=\mathrm{xln}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)−\int\:\mathrm{x}×\frac{\mathrm{2x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\mathrm{xln}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)−\mathrm{2}\:\int\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\mathrm{xln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)−\mathrm{2x}\:+\mathrm{2arctanx}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{xlnx}−\mathrm{x}−\frac{\mathrm{x}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)+\mathrm{x}\:−\mathrm{arctanx}\:\:+\mathrm{kx}\:+\mathrm{c}\:\: \\ $$$$\mathrm{c}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}−\mathrm{cost}}{\mathrm{t}^{\mathrm{2}} }\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{t}}{\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\mathrm{2}\left\{\:\:\left[−\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{t}}{\mathrm{t}}\right]_{\mathrm{0}} ^{\infty} +\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2sintcost}}{\mathrm{t}}\:\mathrm{dt}\right\}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{2t}\right)}{\mathrm{t}}\:\mathrm{dt}\:=_{\mathrm{2t}=\mathrm{u}} \:\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sinu}}{\frac{\mathrm{u}}{\mathrm{2}}}×\frac{\mathrm{du}}{\mathrm{2}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sinu}}{\mathrm{u}}\mathrm{du}\:=\pi\:\Rightarrow\mathrm{c}\:=\pi\:\:\mathrm{rest}\:\mathrm{to}\:\mathrm{find}\:\mathrm{k}\:….\mathrm{be}\:\mathrm{continued}…. \\ $$$$ \\ $$
