Question Number 158081 by Eric002 last updated on 30/Oct/21
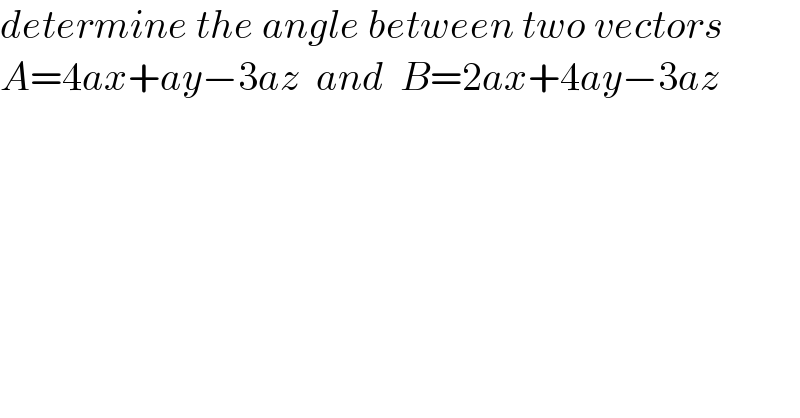
$${determine}\:{the}\:{angle}\:{between}\:{two}\:{vectors} \\ $$$${A}=\mathrm{4}{ax}+{ay}−\mathrm{3}{az}\:\:{and}\:\:{B}=\mathrm{2}{ax}+\mathrm{4}{ay}−\mathrm{3}{az} \\ $$
Answered by ajfour last updated on 30/Oct/21
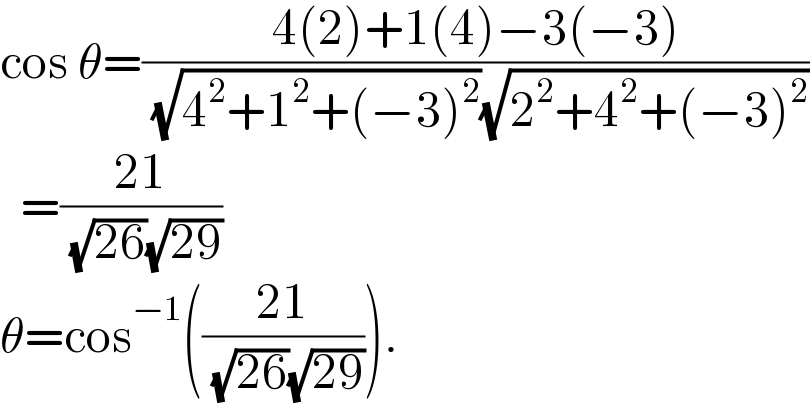
$$\mathrm{cos}\:\theta=\frac{\mathrm{4}\left(\mathrm{2}\right)+\mathrm{1}\left(\mathrm{4}\right)−\mathrm{3}\left(−\mathrm{3}\right)}{\:\sqrt{\mathrm{4}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} +\left(−\mathrm{3}\right)^{\mathrm{2}} }\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} +\left(−\mathrm{3}\right)^{\mathrm{2}} }} \\ $$$$\:\:=\frac{\mathrm{21}}{\:\sqrt{\mathrm{26}}\sqrt{\mathrm{29}}} \\ $$$$\theta=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{21}}{\:\sqrt{\mathrm{26}}\sqrt{\mathrm{29}}}\right). \\ $$
