Menu Close

Determine-the-fourth-roots-of-16-giving-the-results-in-polar-form-and-in-exponential-form-Answers-2-1-j-2-1-j-2-1-j-2-1-j-

Tinku Tara 0 Comments
Pin




Question Number 50806 by Tawa1 last updated on 20/Dec/18
Determine the fourth roots of − 16 , giving the results in polar form and in exponential form Answers: (√2) (1 + j) , (√2) (− 1 + j) , (√2) (− 1 − j), (√2)(1 − j)
$$\mathrm{Determine}\:\mathrm{the}\:\mathrm{fourth}\:\mathrm{roots}\:\mathrm{of}\:\:−\:\mathrm{16}\:,\:\:\mathrm{giving}\:\mathrm{the}\:\mathrm{results}\:\mathrm{in}\:\mathrm{polar} \\ $$$$\mathrm{form}\:\mathrm{and}\:\mathrm{in}\:\mathrm{exponential}\:\mathrm{form} \\ $$$$\boldsymbol{\mathrm{Answers}}:\:\:\:\:\:\sqrt{\mathrm{2}}\:\left(\mathrm{1}\:+\:\boldsymbol{\mathrm{j}}\right)\:,\:\:\sqrt{\mathrm{2}}\:\left(−\:\mathrm{1}\:+\:\boldsymbol{\mathrm{j}}\right)\:,\:\:\:\:\:\sqrt{\mathrm{2}}\:\left(−\:\mathrm{1}\:−\:\boldsymbol{\mathrm{j}}\right),\:\:\:\:\sqrt{\mathrm{2}}\left(\mathrm{1}\:−\:\boldsymbol{\mathrm{j}}\right) \\ $$
Answered by mr W last updated on 20/Dec/18
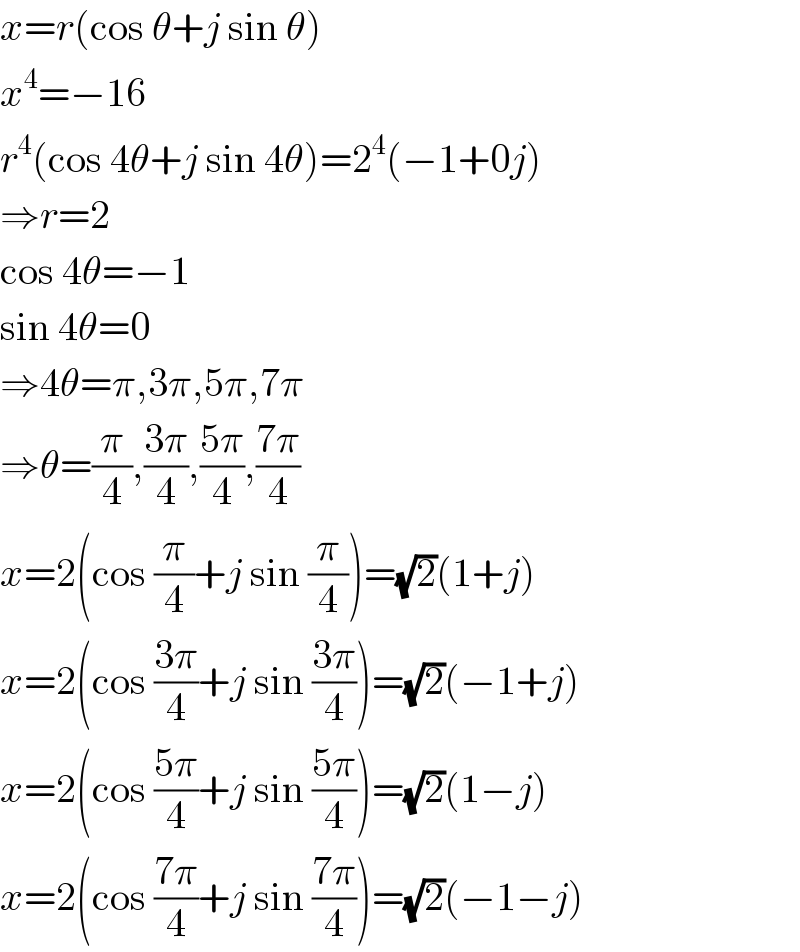
x=r(cos θ+j sin θ) x^4 =−16 r^4 (cos 4θ+j sin 4θ)=2^4 (−1+0j) ⇒r=2 cos 4θ=−1 sin 4θ=0 ⇒4θ=π,3π,5π,7π ⇒θ=(π/4),((3π)/4),((5π)/4),((7π)/4) x=2(cos (π/4)+j sin (π/4))=(√2)(1+j) x=2(cos ((3π)/4)+j sin ((3π)/4))=(√2)(−1+j) x=2(cos ((5π)/4)+j sin ((5π)/4))=(√2)(1−j) x=2(cos ((7π)/4)+j sin ((7π)/4))=(√2)(−1−j)
$${x}={r}\left(\mathrm{cos}\:\theta+{j}\:\mathrm{sin}\:\theta\right) \\ $$$${x}^{\mathrm{4}} =−\mathrm{16} \\ $$$${r}^{\mathrm{4}} \left(\mathrm{cos}\:\mathrm{4}\theta+{j}\:\mathrm{sin}\:\mathrm{4}\theta\right)=\mathrm{2}^{\mathrm{4}} \left(−\mathrm{1}+\mathrm{0}{j}\right) \\ $$$$\Rightarrow{r}=\mathrm{2} \\ $$$$\mathrm{cos}\:\mathrm{4}\theta=−\mathrm{1} \\ $$$$\mathrm{sin}\:\mathrm{4}\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}\theta=\pi,\mathrm{3}\pi,\mathrm{5}\pi,\mathrm{7}\pi \\ $$$$\Rightarrow\theta=\frac{\pi}{\mathrm{4}},\frac{\mathrm{3}\pi}{\mathrm{4}},\frac{\mathrm{5}\pi}{\mathrm{4}},\frac{\mathrm{7}\pi}{\mathrm{4}} \\ $$$${x}=\mathrm{2}\left(\mathrm{cos}\:\frac{\pi}{\mathrm{4}}+{j}\:\mathrm{sin}\:\frac{\pi}{\mathrm{4}}\right)=\sqrt{\mathrm{2}}\left(\mathrm{1}+{j}\right) \\ $$$${x}=\mathrm{2}\left(\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{4}}+{j}\:\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{4}}\right)=\sqrt{\mathrm{2}}\left(−\mathrm{1}+{j}\right) \\ $$$${x}=\mathrm{2}\left(\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{4}}+{j}\:\mathrm{sin}\:\frac{\mathrm{5}\pi}{\mathrm{4}}\right)=\sqrt{\mathrm{2}}\left(\mathrm{1}−{j}\right) \\ $$$${x}=\mathrm{2}\left(\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{4}}+{j}\:\mathrm{sin}\:\frac{\mathrm{7}\pi}{\mathrm{4}}\right)=\sqrt{\mathrm{2}}\left(−\mathrm{1}−{j}\right) \\ $$
Commented by Tawa1 last updated on 20/Dec/18
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 21/Dec/18
Sir, am trying to understand how you got 3π, 5π, 7π ... I thought the angles should be in the same interval sir. like in interval of ((360)/4) = 90 since it is 4th roots. so, 4θ = 180, 270, 360, 450, etc ... Please sir, i want to know why we use π, 3π, 5π, 7π, and not the interval of 4th roots ((360)/4) = 90. God bless you sir
$$\mathrm{Sir},\:\mathrm{am}\:\mathrm{trying}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{how}\:\mathrm{you}\:\mathrm{got}\:\:\mathrm{3}\pi,\:\mathrm{5}\pi,\:\mathrm{7}\pi\:… \\ $$$$\mathrm{I}\:\mathrm{thought}\:\mathrm{the}\:\mathrm{angles}\:\mathrm{should}\:\mathrm{be}\:\mathrm{in}\:\mathrm{the}\:\mathrm{same}\:\mathrm{interval}\:\mathrm{sir}.\:\:\mathrm{like}\:\mathrm{in}\: \\ $$$$\mathrm{interval}\:\mathrm{of}\:\:\:\:\:\:\frac{\mathrm{360}}{\mathrm{4}}\:\:=\:\:\mathrm{90}\:\:\:\:\:\mathrm{since}\:\mathrm{it}\:\mathrm{is}\:\mathrm{4th}\:\mathrm{roots}. \\ $$$$\mathrm{so},\:\:\mathrm{4}\theta\:\:=\:\:\mathrm{180},\:\mathrm{270},\:\mathrm{360},\:\mathrm{450},\:\:\mathrm{etc}\:…\:\: \\ $$$$ \\ $$$$\mathrm{Please}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{want}\:\mathrm{to}\:\mathrm{know}\:\mathrm{why}\:\mathrm{we}\:\mathrm{use}\:\:\:\pi,\:\mathrm{3}\pi,\:\mathrm{5}\pi,\:\mathrm{7}\pi,\:\:\:\mathrm{and}\:\mathrm{not}\:\mathrm{the}\: \\ $$$$\mathrm{interval}\:\mathrm{of}\:\mathrm{4th}\:\mathrm{roots}\:\:\:\frac{\mathrm{360}}{\mathrm{4}}\:\:=\:\mathrm{90}. \\ $$$$ \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 21/Dec/18
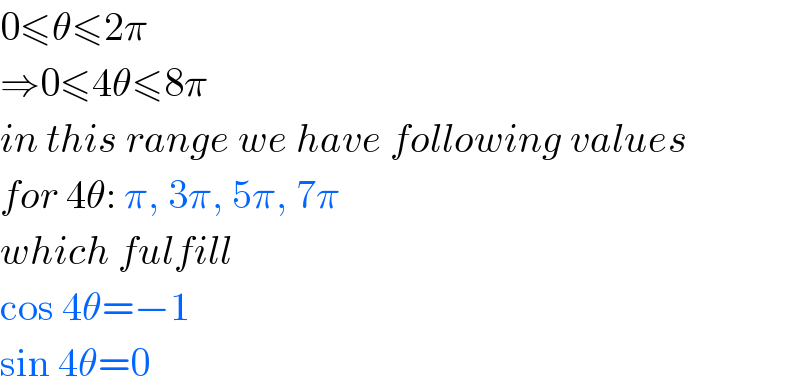
0≤θ≤2π ⇒0≤4θ≤8π in this range we have following values for 4θ: π, 3π, 5π, 7π which fulfill cos 4θ=−1 sin 4θ=0
$$\mathrm{0}\leqslant\theta\leqslant\mathrm{2}\pi \\ $$$$\Rightarrow\mathrm{0}\leqslant\mathrm{4}\theta\leqslant\mathrm{8}\pi \\ $$$${in}\:{this}\:{range}\:{we}\:{have}\:{following}\:{values} \\ $$$${for}\:\mathrm{4}\theta:\:\pi,\:\mathrm{3}\pi,\:\mathrm{5}\pi,\:\mathrm{7}\pi \\ $$$${which}\:{fulfill} \\ $$$$\mathrm{cos}\:\mathrm{4}\theta=−\mathrm{1} \\ $$$$\mathrm{sin}\:\mathrm{4}\theta=\mathrm{0} \\ $$
Answered by peter frank last updated on 21/Dec/18
z^4 =−16(cos π+jsin π) r=(√(16^2 )) =16 from z_k =r^(1/n) [cos ((θ+2πk)/n)+jsin ((θ+2πk)/n)] n=4 θ=π z_k =2[cos ((π+2πk)/4)+jsin ((π+2πk)/4)] k=0 z_0 =2(cos (π/4)+jsin (π/4))=(√2) (1+j) k=1 z_1 =2(cos ((3π)/4)+jsin ((3π)/4))=-(√2) (1−j) k=2 z_2 =2(cos ((5π)/4)+jsin ((5π)/4))=(√2) (-1−j) k=3 z_3 =2(cos ((7π)/4)+jsin ((7π)/4))=(√(2 ))(1−j)
$$\:{z}^{\mathrm{4}} =−\mathrm{16}\left(\mathrm{cos}\:\pi+{j}\mathrm{sin}\:\pi\right) \\ $$$${r}=\sqrt{\mathrm{16}^{\mathrm{2}} }\:=\mathrm{16} \\ $$$${from}\: \\ $$$${z}_{{k}} ={r}^{\frac{\mathrm{1}}{{n}}} \left[\mathrm{cos}\:\frac{\theta+\mathrm{2}\pi{k}}{{n}}+{j}\mathrm{sin}\:\frac{\theta+\mathrm{2}\pi{k}}{{n}}\right] \\ $$$${n}=\mathrm{4}\:\:\:\:\:\:\theta=\pi \\ $$$${z}_{{k}} =\mathrm{2}\left[\mathrm{cos}\:\frac{\pi+\mathrm{2}\pi{k}}{\mathrm{4}}+{j}\mathrm{sin}\:\frac{\pi+\mathrm{2}\pi{k}}{\mathrm{4}}\right] \\ $$$${k}=\mathrm{0} \\ $$$${z}_{\mathrm{0}} =\mathrm{2}\left(\mathrm{cos}\:\frac{\pi}{\mathrm{4}}+{j}\mathrm{sin}\:\frac{\pi}{\mathrm{4}}\right)=\sqrt{\mathrm{2}}\:\left(\mathrm{1}+{j}\right) \\ $$$$\mathrm{k}=\mathrm{1} \\ $$$${z}_{\mathrm{1}} =\mathrm{2}\left(\mathrm{cos}\:\:\frac{\mathrm{3}\pi}{\mathrm{4}}+{j}\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{4}}\right)=-\sqrt{\mathrm{2}}\:\left(\mathrm{1}−{j}\right) \\ $$$${k}=\mathrm{2} \\ $$$${z}_{\mathrm{2}} =\mathrm{2}\left(\mathrm{cos}\:\:\frac{\mathrm{5}\pi}{\mathrm{4}}+{j}\mathrm{sin}\:\frac{\mathrm{5}\pi}{\mathrm{4}}\right)=\sqrt{\mathrm{2}}\:\left(-\mathrm{1}−{j}\right) \\ $$$${k}=\mathrm{3} \\ $$$${z}_{\mathrm{3}} =\mathrm{2}\left(\mathrm{cos}\:\:\frac{\mathrm{7}\pi}{\mathrm{4}}+{j}\mathrm{sin}\:\frac{\mathrm{7}\pi}{\mathrm{4}}\right)=\sqrt{\mathrm{2}\:}\left(\mathrm{1}−{j}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by Tawa1 last updated on 21/Dec/18
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *