Menu Close

Determine-the-roots-of-the-equation-x-3-64-0-in-the-polar-form-a-jb-Where-a-and-b-are-real-

Tinku Tara 0 Comments
Pin




Question Number 14587 by tawa tawa last updated on 02/Jun/17
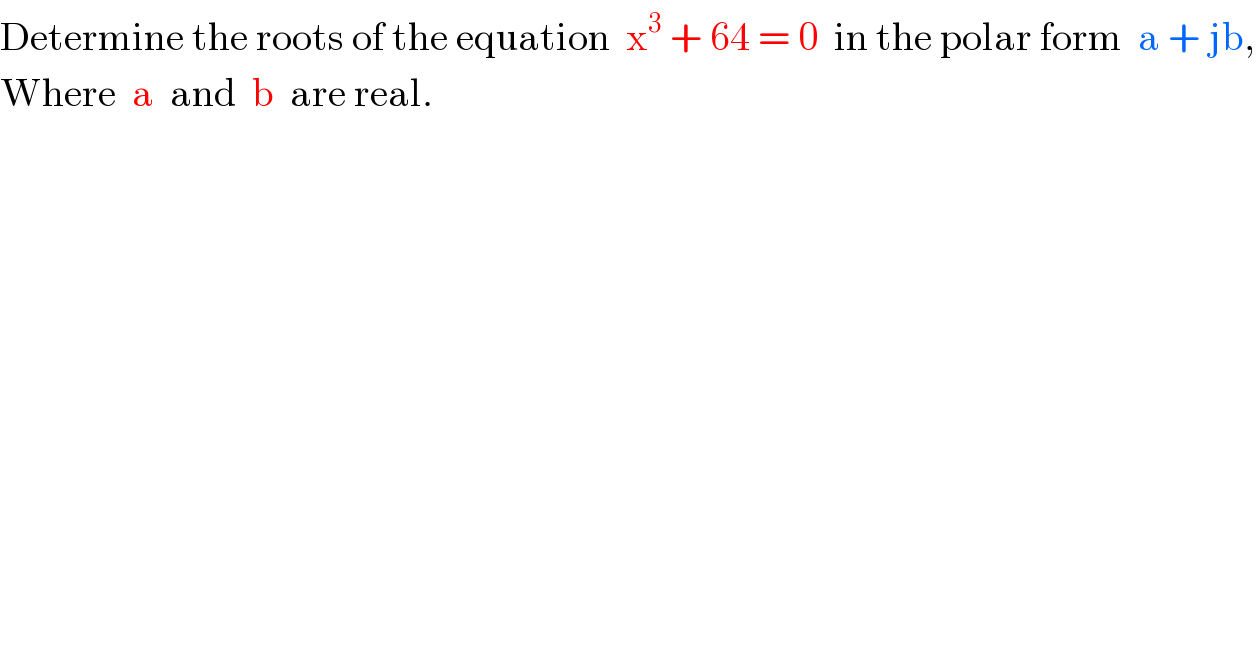
Determine the roots of the equation x^3 + 64 = 0 in the polar form a + jb, Where a and b are real.
$$\mathrm{Determine}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\:\:\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{64}\:=\:\mathrm{0}\:\:\mathrm{in}\:\mathrm{the}\:\mathrm{polar}\:\mathrm{form}\:\:\mathrm{a}\:+\:\mathrm{jb}, \\ $$$$\mathrm{Where}\:\:\mathrm{a}\:\:\mathrm{and}\:\:\mathrm{b}\:\:\mathrm{are}\:\mathrm{real}. \\ $$
Answered by mrW1 last updated on 03/Jun/17
x=r(cos θ+i sin θ) x^3 =r^3 (cos 3ϑ+i sin 3θ)=−64=64(−1+0 i) ⇒r^3 =64⇒r=^3 (√(64))=4 ⇒cos 3θ=−1 ⇒sin 3θ=0 ⇒3θ=(2n−1)π, n=1,2,3 ⇒θ_1 =(π/3) ⇒θ_2 =π ⇒θ_3 =((5π)/3) x_1 =4(cos (π/3)+i sin (π/3))=2+2(√3) i x_2 =4(cos π+i sin π)=−4+0 i x_3 =4(cos ((5π)/3)+i sin ((5π)/3))=2−2(√3) i
$${x}={r}\left(\mathrm{cos}\:\theta+{i}\:\mathrm{sin}\:\theta\right) \\ $$$${x}^{\mathrm{3}} ={r}^{\mathrm{3}} \left(\mathrm{cos}\:\mathrm{3}\vartheta+{i}\:\mathrm{sin}\:\mathrm{3}\theta\right)=−\mathrm{64}=\mathrm{64}\left(−\mathrm{1}+\mathrm{0}\:{i}\right) \\ $$$$\Rightarrow{r}^{\mathrm{3}} =\mathrm{64}\Rightarrow{r}=\:^{\mathrm{3}} \sqrt{\mathrm{64}}=\mathrm{4} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{3}\theta=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{3}\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{3}\theta=\left(\mathrm{2}{n}−\mathrm{1}\right)\pi,\:{n}=\mathrm{1},\mathrm{2},\mathrm{3} \\ $$$$\Rightarrow\theta_{\mathrm{1}} =\frac{\pi}{\mathrm{3}} \\ $$$$\Rightarrow\theta_{\mathrm{2}} =\pi \\ $$$$\Rightarrow\theta_{\mathrm{3}} =\frac{\mathrm{5}\pi}{\mathrm{3}} \\ $$$${x}_{\mathrm{1}} =\mathrm{4}\left(\mathrm{cos}\:\frac{\pi}{\mathrm{3}}+{i}\:\mathrm{sin}\:\frac{\pi}{\mathrm{3}}\right)=\mathrm{2}+\mathrm{2}\sqrt{\mathrm{3}}\:{i} \\ $$$${x}_{\mathrm{2}} =\mathrm{4}\left(\mathrm{cos}\:\pi+{i}\:\mathrm{sin}\:\pi\right)=−\mathrm{4}+\mathrm{0}\:{i} \\ $$$${x}_{\mathrm{3}} =\mathrm{4}\left(\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{3}}+{i}\:\mathrm{sin}\:\frac{\mathrm{5}\pi}{\mathrm{3}}\right)=\mathrm{2}−\mathrm{2}\sqrt{\mathrm{3}}\:{i} \\ $$
Commented by RasheedSoomro last updated on 04/Jun/17
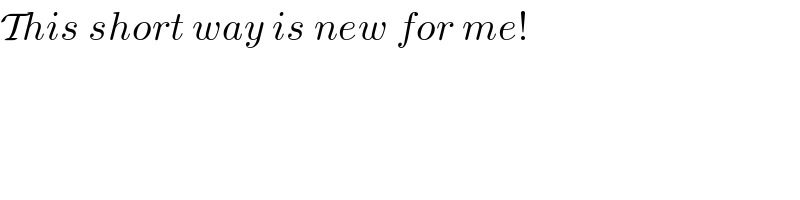
This short way is new for me!
$$\mathcal{T}{his}\:{short}\:{way}\:{is}\:{new}\:{for}\:{me}! \\ $$
Commented by mrW1 last updated on 03/Jun/17
or x^3 =−64 ((x/(−4)))^3 =1 ⇒(x/(−4))=1,ω,ω^2 ⇒x=−4,−4ω,−4ω^2
$${or} \\ $$$${x}^{\mathrm{3}} =−\mathrm{64} \\ $$$$\left(\frac{{x}}{−\mathrm{4}}\right)^{\mathrm{3}} =\mathrm{1} \\ $$$$\Rightarrow\frac{{x}}{−\mathrm{4}}=\mathrm{1},\omega,\omega^{\mathrm{2}} \\ $$$$\Rightarrow{x}=−\mathrm{4},−\mathrm{4}\omega,−\mathrm{4}\omega^{\mathrm{2}} \\ $$
Commented by tawa tawa last updated on 04/Jun/17
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by tawa tawa last updated on 04/Jun/17
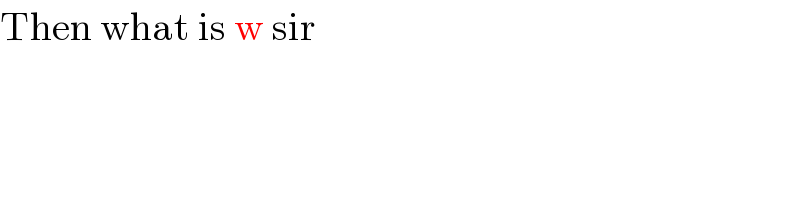
Then what is w sir
$$\mathrm{Then}\:\mathrm{what}\:\mathrm{is}\:\mathrm{w}\:\mathrm{sir} \\ $$
Commented by Tinkutara last updated on 04/Jun/17
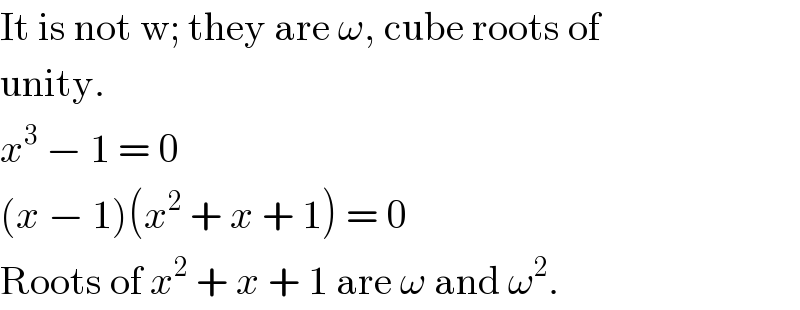
It is not w; they are ω, cube roots of unity. x^3 − 1 = 0 (x − 1)(x^2 + x + 1) = 0 Roots of x^2 + x + 1 are ω and ω^2 .
$$\mathrm{It}\:\mathrm{is}\:\mathrm{not}\:\mathrm{w};\:\mathrm{they}\:\mathrm{are}\:\omega,\:\mathrm{cube}\:\mathrm{roots}\:\mathrm{of} \\ $$$$\mathrm{unity}. \\ $$$${x}^{\mathrm{3}} \:−\:\mathrm{1}\:=\:\mathrm{0} \\ $$$$\left({x}\:−\:\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\:{x}\:+\:\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{Roots}\:\mathrm{of}\:{x}^{\mathrm{2}} \:+\:{x}\:+\:\mathrm{1}\:\mathrm{are}\:\omega\:\mathrm{and}\:\omega^{\mathrm{2}} . \\ $$
Commented by tawa tawa last updated on 04/Jun/17
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mrW1 last updated on 04/Jun/17
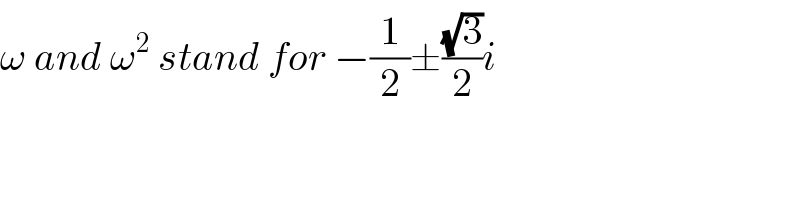
ω and ω^2 stand for −(1/2)±((√3)/2)i
$$\omega\:{and}\:\omega^{\mathrm{2}} \:{stand}\:{for}\:−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i} \\ $$
Commented by tawa tawa last updated on 04/Jun/17
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by tawa tawa last updated on 04/Jun/17
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by arnabpapu550@gmail.com last updated on 13/Jun/17
To dear tawa. To find the qube root of 1 put x^3 =1 ∴ x^3 −1=0 or, (x−1)(x^2 +x+1)=0 ∴ (x−1)=0 ⇒x=1 or, (x^2 +x+1)=0 ∴ x=((−1±(√(1−4.1.1 )))/2)=((−1±i(√3))/2) It is denoted by ω and ω^2 . Where ω=((−1+i(√3))/2) ω^2 =((−1−i(√3))/2) [You may varify it] Properties: (a) ω^3 =1 ∴ ω^4 =ω^3 .ω=ω (b) 1+ω+ω^2 =0
$$\mathrm{To}\:\mathrm{dear}\:\mathrm{tawa}. \\ $$$$\mathrm{To}\:\mathrm{find}\:\mathrm{the}\:\mathrm{qube}\:\mathrm{root}\:\mathrm{of}\:\mathrm{1}\:\mathrm{put}\:\mathrm{x}^{\mathrm{3}} =\mathrm{1} \\ $$$$\therefore\:\mathrm{x}^{\mathrm{3}} −\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{or},\:\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\therefore\:\left(\mathrm{x}−\mathrm{1}\right)=\mathrm{0}\:\Rightarrow\mathrm{x}=\mathrm{1} \\ $$$$\mathrm{or},\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\therefore\:\:\mathrm{x}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{4}.\mathrm{1}.\mathrm{1}\:}}{\mathrm{2}}=\frac{−\mathrm{1}\pm\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{denoted}\:\mathrm{by}\:\omega\:\mathrm{and}\:\omega^{\mathrm{2}} . \\ $$$$\mathrm{Where}\:\omega=\frac{−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\omega^{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\left[\mathrm{You}\:\mathrm{may}\:\mathrm{varify}\:\mathrm{it}\right] \\ $$$$\mathrm{Properties}: \\ $$$$\left(\mathrm{a}\right)\:\omega^{\mathrm{3}} =\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\therefore\:\omega^{\mathrm{4}} =\omega^{\mathrm{3}} .\omega=\omega \\ $$$$\left(\mathrm{b}\right)\:\mathrm{1}+\omega+\omega^{\mathrm{2}} =\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *