Question Number 79131 by mathocean1 last updated on 23/Jan/20
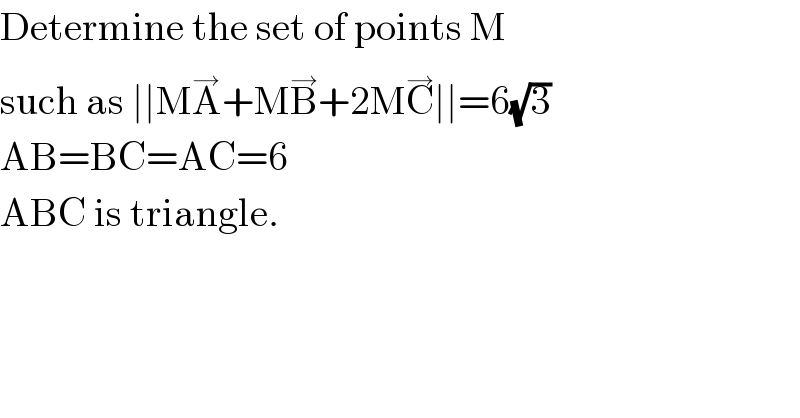
$$\mathrm{Determine}\:\mathrm{the}\:\mathrm{set}\:\mathrm{of}\:\mathrm{points}\:\mathrm{M}\: \\ $$$$\mathrm{such}\:\mathrm{as}\:\mid\mid\mathrm{M}\overset{\rightarrow} {\mathrm{A}}+\mathrm{M}\overset{\rightarrow} {\mathrm{B}}+\mathrm{2M}\overset{\rightarrow} {\mathrm{C}}\mid\mid=\mathrm{6}\sqrt{\mathrm{3}} \\ $$$$\mathrm{AB}=\mathrm{BC}=\mathrm{AC}=\mathrm{6} \\ $$$$\mathrm{ABC}\:\mathrm{is}\:\mathrm{triangle}. \\ $$
Commented by mathocean1 last updated on 23/Jan/20

$$\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{sirs} \\ $$
Commented by msup trace by abdo last updated on 23/Jan/20
![let G =barycentre of the system {(A,1),(B,1) ,(C,2)} (e) ⇔∣∣4MG^→ ∣∣=6(√3)⇒MG=((6(√3))/4) ⇒MG=((3(√3))/2) ⇒M varie on cercle C(G,((3(√3))/2)) how to trace G? G is bsrycentre of { (I,2),(C,2)} with I midpoint of [A,B] ⇒G midpoint of [I,C]....](https://www.tinkutara.com/question/Q79234.png)
$${let}\:{G}\:={barycentre}\:{of}\:{the}\:{system} \\ $$$$\left\{\left({A},\mathrm{1}\right),\left({B},\mathrm{1}\right)\:,\left({C},\mathrm{2}\right)\right\} \\ $$$$\left({e}\right)\:\Leftrightarrow\mid\mid\mathrm{4}{M}\overset{\rightarrow} {{G}}\mid\mid=\mathrm{6}\sqrt{\mathrm{3}}\Rightarrow{MG}=\frac{\mathrm{6}\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$$\Rightarrow{MG}=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:\Rightarrow{M}\:{varie}\:{on}\:{cercle} \\ $$$${C}\left({G},\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:\:{how}\:{to}\:{trace}\:{G}? \\ $$$${G}\:{is}\:{bsrycentre}\:{of}\:\left\{\:\left({I},\mathrm{2}\right),\left({C},\mathrm{2}\right)\right\} \\ $$$${with}\:{I}\:{midpoint}\:{of}\:\left[{A},{B}\right]\:\Rightarrow{G} \\ $$$${midpoint}\:{of}\:\left[{I},{C}\right]…. \\ $$
Answered by ~blr237~ last updated on 23/Jan/20
![let I be the middle of [AB] and J the middle of [IC] let reduce u^→ =MA^→ +MB^→ +2MC^→ u^→ =MI^→ +IA^→ +MI^→ +IB^→ +2MC^→ =2MI^→ +2MC^→ cause IB^→ =−IA^→ =2(MJ^→ +JI^→ +MJ^→ +JC^→ ) =4MJ^→ cause J middle of [IC] The search point must satisfy ∣∣4MJ^→ ∣∣=6(√3) ⇔ MJ=((3(√3))/2) Finaly the searched set is the circle whose center is J and radius is ((3(√3))/2)](https://www.tinkutara.com/question/Q79166.png)
$${let}\:{I}\:{be}\:{the}\:{middle}\:{of}\:\left[{AB}\right]\:{and}\:{J}\:{the}\:{middle}\:{of}\:\left[{IC}\right] \\ $$$${let}\:{reduce}\:\overset{\rightarrow} {{u}}={M}\overset{\rightarrow} {{A}}+{M}\overset{\rightarrow} {{B}}+\mathrm{2}{M}\overset{\rightarrow} {{C}} \\ $$$$\overset{\rightarrow} {{u}}={M}\overset{\rightarrow} {{I}}+{I}\overset{\rightarrow} {{A}}+{M}\overset{\rightarrow} {{I}}+{I}\overset{\rightarrow} {{B}}+\mathrm{2}{M}\overset{\rightarrow} {{C}} \\ $$$$\:\:\:\:=\mathrm{2}{M}\overset{\rightarrow} {{I}}+\mathrm{2}{M}\overset{\rightarrow} {{C}}\:\:\:{cause}\:\:{I}\overset{\rightarrow} {{B}}=−{I}\overset{\rightarrow} {{A}} \\ $$$$\:\:\:\:=\mathrm{2}\left({M}\overset{\rightarrow} {{J}}+{J}\overset{\rightarrow} {{I}}+{M}\overset{\rightarrow} {{J}}+{J}\overset{\rightarrow} {{C}}\right) \\ $$$$\:\:\:\:=\mathrm{4}{M}\overset{\rightarrow} {{J}}\:\:\:\:{cause}\:\:{J}\:{middle}\:{of}\:\left[{IC}\right] \\ $$$${The}\:{search}\:{point}\:{must}\:{satisfy}\:\:\mid\mid\mathrm{4}{M}\overset{\rightarrow} {{J}}\mid\mid=\mathrm{6}\sqrt{\mathrm{3}}\:\Leftrightarrow\:{MJ}=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\: \\ $$$${Finaly}\:{the}\:{searched}\:{set}\:{is}\:{the}\:{circle}\:{whose}\:{center}\:{is}\:{J}\:{and}\:{radius}\:{is}\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\: \\ $$$$ \\ $$
