Question Number 117852 by bemath last updated on 14/Oct/20
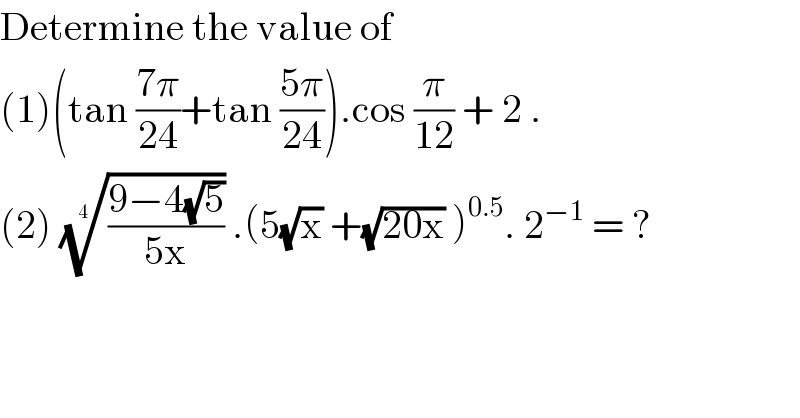
$$\mathrm{Determine}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\: \\ $$$$\left(\mathrm{1}\right)\left(\mathrm{tan}\:\frac{\mathrm{7}\pi}{\mathrm{24}}+\mathrm{tan}\:\frac{\mathrm{5}\pi}{\mathrm{24}}\right).\mathrm{cos}\:\frac{\pi}{\mathrm{12}}\:+\:\mathrm{2}\:. \\ $$$$\left(\mathrm{2}\right)\:\sqrt[{\mathrm{4}\:}]{\frac{\mathrm{9}−\mathrm{4}\sqrt{\mathrm{5}}}{\mathrm{5x}}}\:.\left(\mathrm{5}\sqrt{\mathrm{x}}\:+\sqrt{\mathrm{20x}}\:\right)^{\mathrm{0}.\mathrm{5}} .\:\mathrm{2}^{−\mathrm{1}} \:=\:? \\ $$
Answered by bobhans last updated on 14/Oct/20
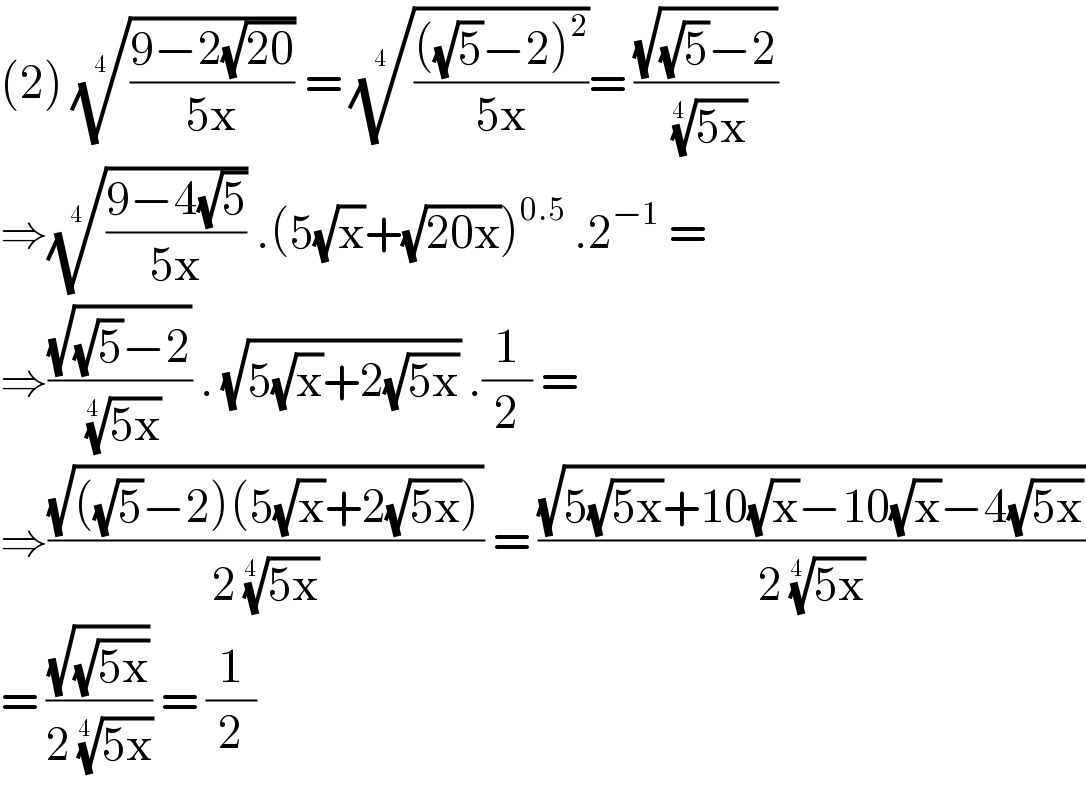
$$\left(\mathrm{2}\right)\:\sqrt[{\mathrm{4}\:}]{\frac{\mathrm{9}−\mathrm{2}\sqrt{\mathrm{20}}}{\mathrm{5x}}}\:=\:\sqrt[{\mathrm{4}\:}]{\frac{\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{5x}}}=\:\frac{\sqrt{\sqrt{\mathrm{5}}−\mathrm{2}}}{\:\sqrt[{\mathrm{4}\:}]{\mathrm{5x}}} \\ $$$$\Rightarrow\sqrt[{\mathrm{4}\:}]{\frac{\mathrm{9}−\mathrm{4}\sqrt{\mathrm{5}}}{\mathrm{5x}}}\:.\left(\mathrm{5}\sqrt{\mathrm{x}}+\sqrt{\mathrm{20x}}\right)^{\mathrm{0}.\mathrm{5}} \:.\mathrm{2}^{−\mathrm{1}} \:= \\ $$$$\Rightarrow\frac{\sqrt{\sqrt{\mathrm{5}}−\mathrm{2}}}{\:\sqrt[{\mathrm{4}\:}]{\mathrm{5x}}}\:.\:\sqrt{\mathrm{5}\sqrt{\mathrm{x}}+\mathrm{2}\sqrt{\mathrm{5x}}}\:.\frac{\mathrm{1}}{\mathrm{2}}\:=\: \\ $$$$\Rightarrow\frac{\sqrt{\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)\left(\mathrm{5}\sqrt{\mathrm{x}}+\mathrm{2}\sqrt{\mathrm{5x}}\right)}}{\mathrm{2}\:\sqrt[{\mathrm{4}\:}]{\mathrm{5x}}}\:=\:\frac{\sqrt{\mathrm{5}\sqrt{\mathrm{5x}}+\mathrm{10}\sqrt{\mathrm{x}}−\mathrm{10}\sqrt{\mathrm{x}}−\mathrm{4}\sqrt{\mathrm{5x}}}}{\mathrm{2}\:\sqrt[{\mathrm{4}\:}]{\mathrm{5x}}} \\ $$$$=\:\frac{\sqrt{\sqrt{\mathrm{5x}}}}{\mathrm{2}\:\sqrt[{\mathrm{4}\:}]{\mathrm{5x}}}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by bobhans last updated on 14/Oct/20
![(1) letting x = (π/(24)) ⇒(tan 7x+tan 5x).cos 2x +2 = ⇒(((sin 7x.cos 5x+cos 7xsin 5x)/(cos 7x cos 5x))).cos 2x +2 = ⇒((sin 12x)/(2cos 7x cos 5x)). 2cos 2x+2 = ⇒((2cos 2x)/(cos 12x+cos 2x)) + 2 ; [ sin 12x = sin (π/2)=1 ] [ & cos 12x = cos (π/2)=0 ] ⇒ ((2cos (π/(12)))/(cos (π/(12)))) + 2 = 4](https://www.tinkutara.com/question/Q117858.png)
$$\left(\mathrm{1}\right)\:\mathrm{letting}\:\mathrm{x}\:=\:\frac{\pi}{\mathrm{24}} \\ $$$$\Rightarrow\left(\mathrm{tan}\:\mathrm{7x}+\mathrm{tan}\:\mathrm{5x}\right).\mathrm{cos}\:\mathrm{2x}\:+\mathrm{2}\:= \\ $$$$\Rightarrow\left(\frac{\mathrm{sin}\:\mathrm{7x}.\mathrm{cos}\:\mathrm{5x}+\mathrm{cos}\:\mathrm{7xsin}\:\mathrm{5x}}{\mathrm{cos}\:\mathrm{7x}\:\mathrm{cos}\:\mathrm{5x}}\right).\mathrm{cos}\:\mathrm{2x}\:+\mathrm{2}\:= \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\mathrm{12x}}{\mathrm{2cos}\:\mathrm{7x}\:\mathrm{cos}\:\mathrm{5x}}.\:\mathrm{2cos}\:\mathrm{2x}+\mathrm{2}\:= \\ $$$$\Rightarrow\frac{\mathrm{2cos}\:\mathrm{2x}}{\mathrm{cos}\:\mathrm{12x}+\mathrm{cos}\:\mathrm{2x}}\:+\:\mathrm{2}\:;\:\left[\:\mathrm{sin}\:\mathrm{12x}\:=\:\mathrm{sin}\:\frac{\pi}{\mathrm{2}}=\mathrm{1}\:\right] \\ $$$$\left[\:\&\:\mathrm{cos}\:\mathrm{12x}\:=\:\mathrm{cos}\:\frac{\pi}{\mathrm{2}}=\mathrm{0}\:\right] \\ $$$$\Rightarrow\:\frac{\mathrm{2cos}\:\frac{\pi}{\mathrm{12}}}{\mathrm{cos}\:\frac{\pi}{\mathrm{12}}}\:+\:\mathrm{2}\:=\:\mathrm{4} \\ $$
Answered by mindispower last updated on 14/Oct/20
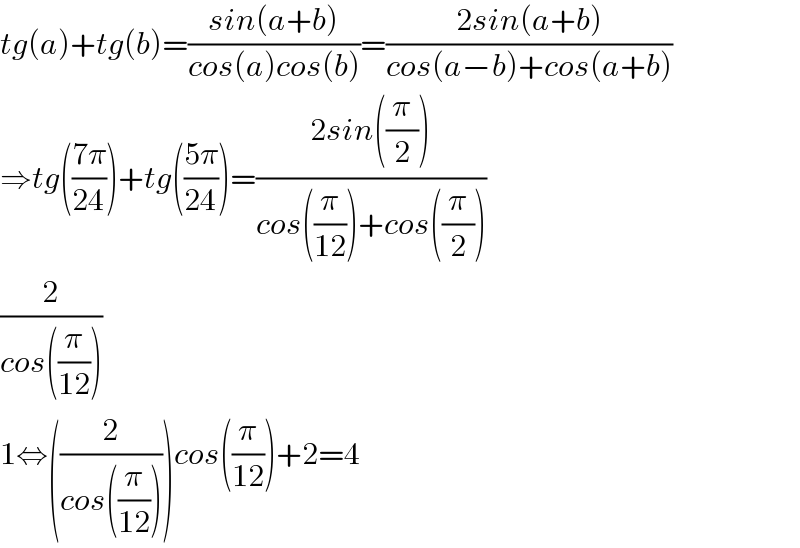
$${tg}\left({a}\right)+{tg}\left({b}\right)=\frac{{sin}\left({a}+{b}\right)}{{cos}\left({a}\right){cos}\left({b}\right)}=\frac{\mathrm{2}{sin}\left({a}+{b}\right)}{{cos}\left({a}−{b}\right)+{cos}\left({a}+{b}\right)} \\ $$$$\Rightarrow{tg}\left(\frac{\mathrm{7}\pi}{\mathrm{24}}\right)+{tg}\left(\frac{\mathrm{5}\pi}{\mathrm{24}}\right)=\frac{\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{2}}\right)}{{cos}\left(\frac{\pi}{\mathrm{12}}\right)+{cos}\left(\frac{\pi}{\mathrm{2}}\right)} \\ $$$$\frac{\mathrm{2}}{{cos}\left(\frac{\pi}{\mathrm{12}}\right)} \\ $$$$\mathrm{1}\Leftrightarrow\left(\frac{\mathrm{2}}{{cos}\left(\frac{\pi}{\mathrm{12}}\right)}\right){cos}\left(\frac{\pi}{\mathrm{12}}\right)+\mathrm{2}=\mathrm{4} \\ $$
