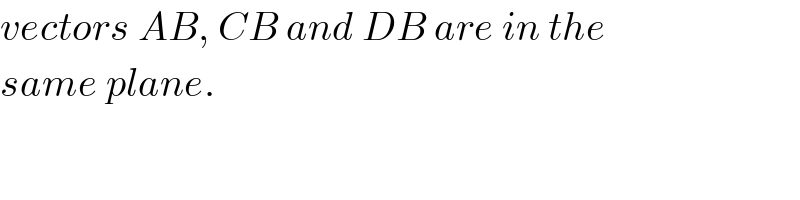Menu Close

determine-the-value-of-k-such-that-the-point-A-4-2-6-B-0-1-0-C-1-0-5-and-D-1-k-2-lie-on-the-same-plane-

Tinku Tara 0 Comments
Pin




Question Number 95342 by i jagooll last updated on 24/May/20
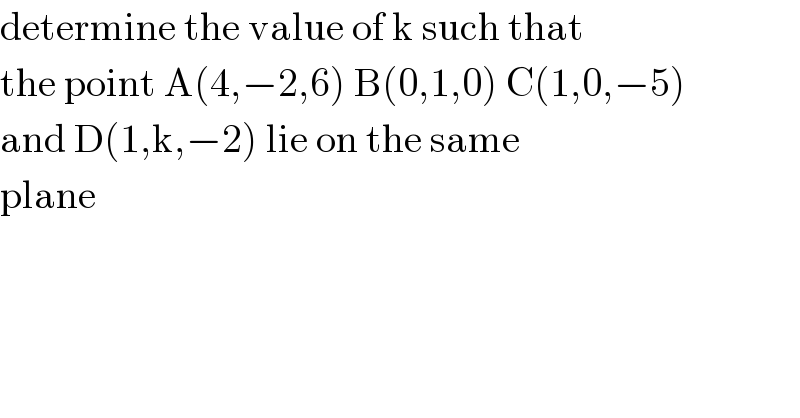
determine the value of k such that the point A(4,−2,6) B(0,1,0) C(1,0,−5) and D(1,k,−2) lie on the same plane
determinethevalueofksuchthatthepointA(4,−2,6)B(0,1,0)C(1,0,−5)andD(1,k,−2)lieonthesameplane
Answered by john santu last updated on 24/May/20
let u = AB=(−4,3,−6) v=(−3,2,−11) . let n vector normal n = u×v = determinant (((−4 3 −6)),((−3 2 −11))) n = (−21,−26,1) . set P(x,y,z) arbitary point in plane. put BP = (x,y−1,z) then the equation of plane is n.BP = 0 −21x−26(y−1)+z = 0 so take x=1,y=k and z = −2 −21.1−26(k−1)−2=0 −21−26k+26−2=0 26k = 3 ⇒ k = (3/(26)) .
letu=AB=(−4,3,−6)v=(−3,2,−11).letnvectornormaln=u×v=|−43−6−32−11|n=(−21,−26,1).setP(x,y,z)arbitarypointinplane.putBP=(x,y−1,z)thentheequationofplaneisn.BP=0−21x−26(y−1)+z=0sotakex=1,y=kandz=−2−21.1−26(k−1)−2=0−21−26k+26−2=026k=3⇒k=326.
Commented by i jagooll last updated on 24/May/20
thank you
thankyou
Answered by mr W last updated on 24/May/20
determinant ((4,(−3),6),(1,(−1),(−5)),(1,(k−1),(−2)))=0 determinant ((4,(−3),6),(0,1,(26)),(0,k,3))=0 4(3−26k)=0 ⇒k=(3/(26))
|4−361−1−51k−1−2|=0|4−3601260k3|=04(3−26k)=0⇒k=326
Commented by i jagooll last updated on 24/May/20
thank you
thankyou
Commented by john santu last updated on 24/May/20
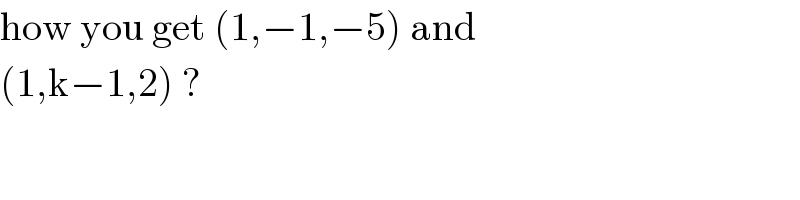
how you get (1,−1,−5) and (1,k−1,2) ?
howyouget(1,−1,−5)and(1,k−1,2)?
Commented by PRITHWISH SEN 2 last updated on 24/May/20
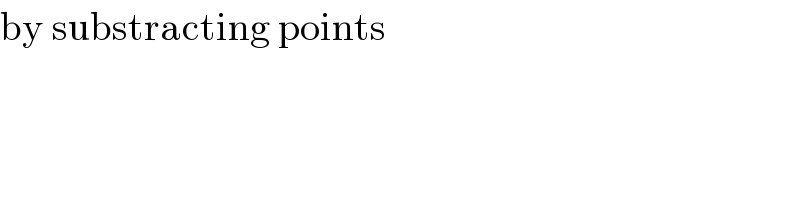
by substracting points
bysubstractingpoints
Commented by john santu last updated on 24/May/20
ooo thank you
ooothankyou
Commented by mr W last updated on 24/May/20
vectors AB, CB and DB are in the same plane.
vectorsAB,CBandDBareinthesameplane.

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *