Question Number 185470 by Mastermind last updated on 22/Jan/23
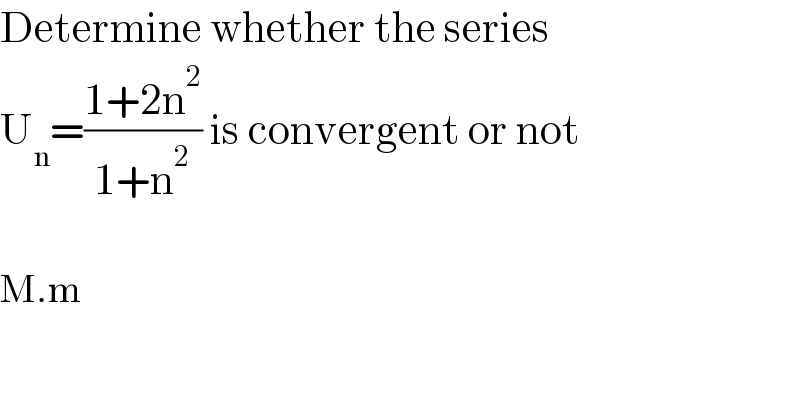
$$\mathrm{Determine}\:\mathrm{whether}\:\mathrm{the}\:\mathrm{series} \\ $$$$\mathrm{U}_{\mathrm{n}} =\frac{\mathrm{1}+\mathrm{2n}^{\mathrm{2}} }{\mathrm{1}+\mathrm{n}^{\mathrm{2}} }\:\mathrm{is}\:\mathrm{convergent}\:\mathrm{or}\:\mathrm{not} \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$
Commented by mr W last updated on 22/Jan/23
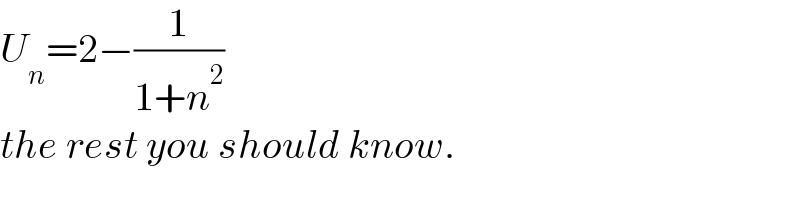
$${U}_{{n}} =\mathrm{2}−\frac{\mathrm{1}}{\mathrm{1}+{n}^{\mathrm{2}} } \\ $$$${the}\:{rest}\:{you}\:{should}\:{know}. \\ $$
Commented by Mastermind last updated on 22/Jan/23

$$\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{series}\:\mathrm{is}\:\mathrm{divergent}\:\mathrm{simply}\: \\ $$$$\mathrm{because}\:\mathrm{A}\:\mathrm{series}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{convergent} \\ $$$$\mathrm{unless}\:\mathrm{it}\:\mathrm{is}\:\mathrm{ultimately}\:\mathrm{tends}\:\mathrm{to}\:\mathrm{zero} \\ $$$$\mathrm{li}\underset{\mathrm{n}\rightarrow\mathrm{0}} {\mathrm{m}U}_{\mathrm{n}} =\mathrm{0}\:\mathrm{converges} \\ $$$$\mathrm{and}\:\mathrm{is}\:\mathrm{not}\:\mathrm{equals}\:\mathrm{zero} \\ $$$$ \\ $$
Commented by Frix last updated on 23/Jan/23

$$\mathrm{Is}\:{U}_{{n}} =\frac{\mathrm{1}+\mathrm{2}{n}^{\mathrm{2}} }{\mathrm{1}+{n}^{\mathrm{2}} }\:\mathrm{a}\:\mathrm{sequence}\:\left(\mathrm{or}\:\mathrm{progression}\right) \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{series}\:\mathrm{we}'\mathrm{re}\:\mathrm{talking}\:\mathrm{about}\:\mathrm{is} \\ $$$${S}_{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{U}_{{k}} \:\mathrm{or}\:\mathrm{is}\:{U}_{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{k}} =\frac{\mathrm{1}+\mathrm{2}{n}^{\mathrm{2}} }{\mathrm{1}+{n}^{\mathrm{2}} }\:\mathrm{and}\:\mathrm{we} \\ $$$$\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\left(\mathrm{and}\:\mathrm{don}'\mathrm{t}\:\mathrm{need}\right)\:{a}_{{n}} ? \\ $$$$\mathrm{In}\:\mathrm{the}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{case}\:{S}_{\infty} =+\infty\:\left(\mathrm{divergent}\right),\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{2}^{\mathrm{nd}} \:\mathrm{case}\:{U}_{\infty} =\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{a}_{{k}} =\mathrm{2}\:\left(\mathrm{convergent}\right). \\ $$
