Question Number 176090 by doline last updated on 11/Sep/22
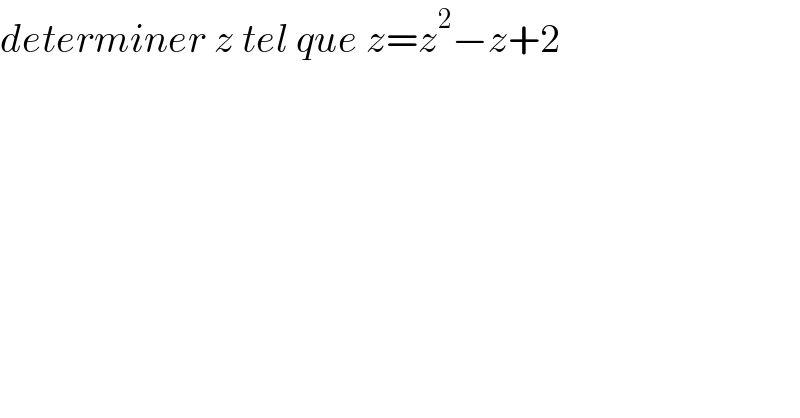
$${determiner}\:{z}\:{tel}\:{que}\:{z}={z}^{\mathrm{2}} −{z}+\mathrm{2} \\ $$$$ \\ $$
Commented by Frix last updated on 12/Sep/22
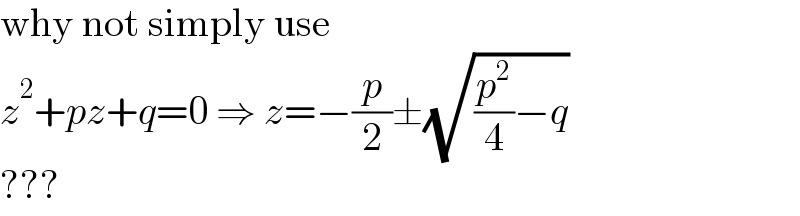
$$\mathrm{why}\:\mathrm{not}\:\mathrm{simply}\:\mathrm{use} \\ $$$${z}^{\mathrm{2}} +{pz}+{q}=\mathrm{0}\:\Rightarrow\:{z}=−\frac{{p}}{\mathrm{2}}\pm\sqrt{\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−{q}} \\ $$$$??? \\ $$
Answered by a.lgnaoui last updated on 12/Sep/22
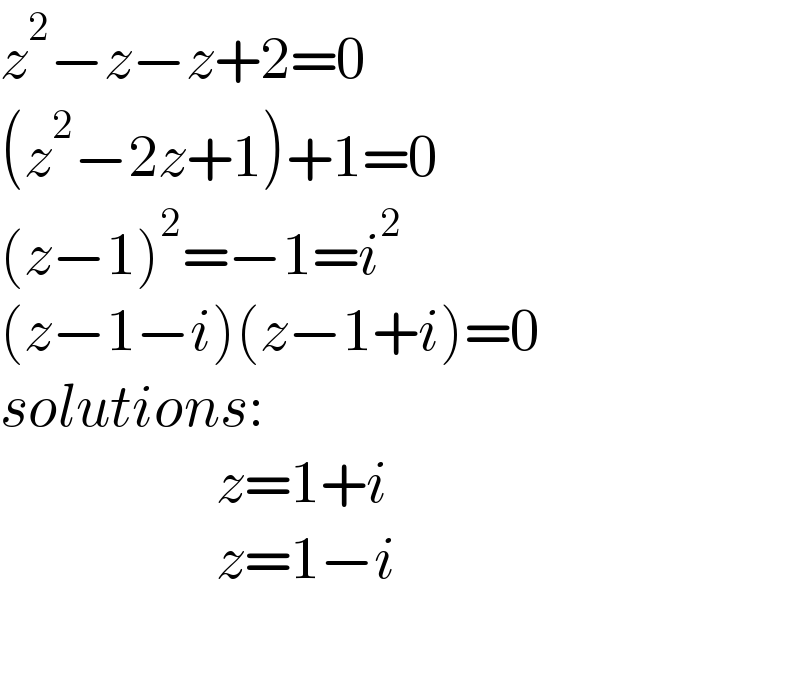
$${z}^{\mathrm{2}} −{z}−{z}+\mathrm{2}=\mathrm{0} \\ $$$$\left({z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{1}\right)+\mathrm{1}=\mathrm{0} \\ $$$$\left({z}−\mathrm{1}\right)^{\mathrm{2}} =−\mathrm{1}={i}^{\mathrm{2}} \\ $$$$\left({z}−\mathrm{1}−{i}\right)\left({z}−\mathrm{1}+{i}\right)=\mathrm{0} \\ $$$${solutions}:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{z}=\mathrm{1}+{i} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{z}=\mathrm{1}−{i} \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 13/Sep/22
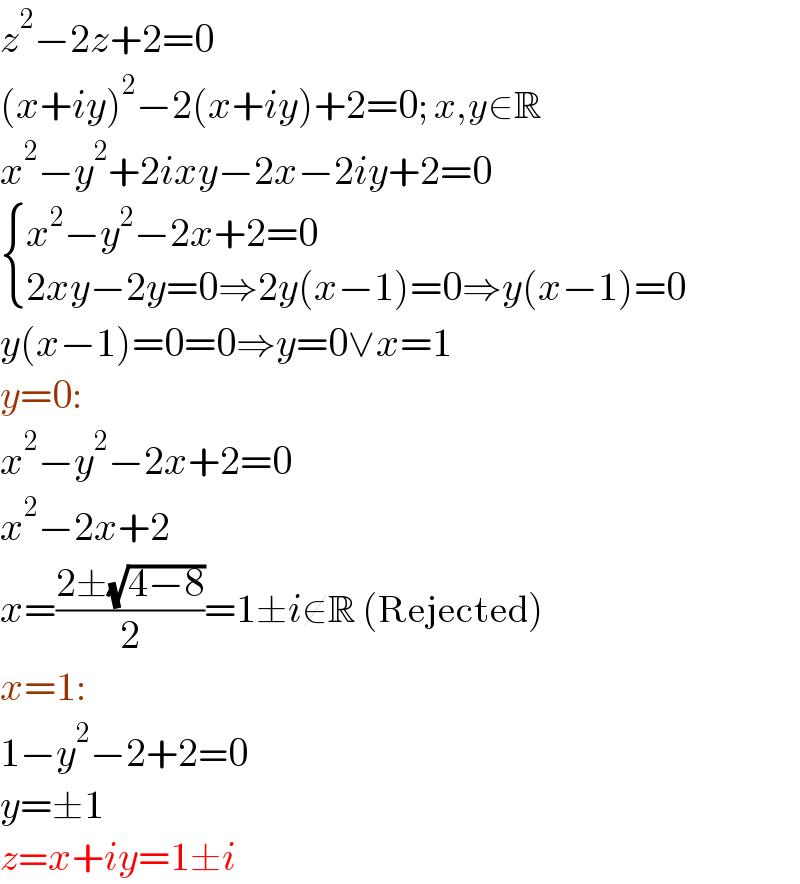
$${z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{2}=\mathrm{0} \\ $$$$\left({x}+{iy}\right)^{\mathrm{2}} −\mathrm{2}\left({x}+{iy}\right)+\mathrm{2}=\mathrm{0};\:{x},{y}\in\mathbb{R} \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} +\mathrm{2}{ixy}−\mathrm{2}{x}−\mathrm{2}{iy}+\mathrm{2}=\mathrm{0} \\ $$$$\begin{cases}{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}=\mathrm{0}}\\{\mathrm{2}{xy}−\mathrm{2}{y}=\mathrm{0}\Rightarrow\mathrm{2}{y}\left({x}−\mathrm{1}\right)=\mathrm{0}\Rightarrow{y}\left({x}−\mathrm{1}\right)=\mathrm{0}}\end{cases} \\ $$$${y}\left({x}−\mathrm{1}\right)=\mathrm{0}=\mathrm{0}\Rightarrow{y}=\mathrm{0}\vee{x}=\mathrm{1} \\ $$$${y}=\mathrm{0}: \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2} \\ $$$${x}=\frac{\mathrm{2}\pm\sqrt{\mathrm{4}−\mathrm{8}}}{\mathrm{2}}=\mathrm{1}\pm{i}\notin\mathbb{R}\:\left(\mathrm{Rejected}\right) \\ $$$${x}=\mathrm{1}: \\ $$$$\mathrm{1}−{y}^{\mathrm{2}} −\mathrm{2}+\mathrm{2}=\mathrm{0} \\ $$$${y}=\pm\mathrm{1} \\ $$$${z}={x}+{iy}=\mathrm{1}\pm{i} \\ $$
