Question Number 62815 by mathmax by abdo last updated on 25/Jun/19
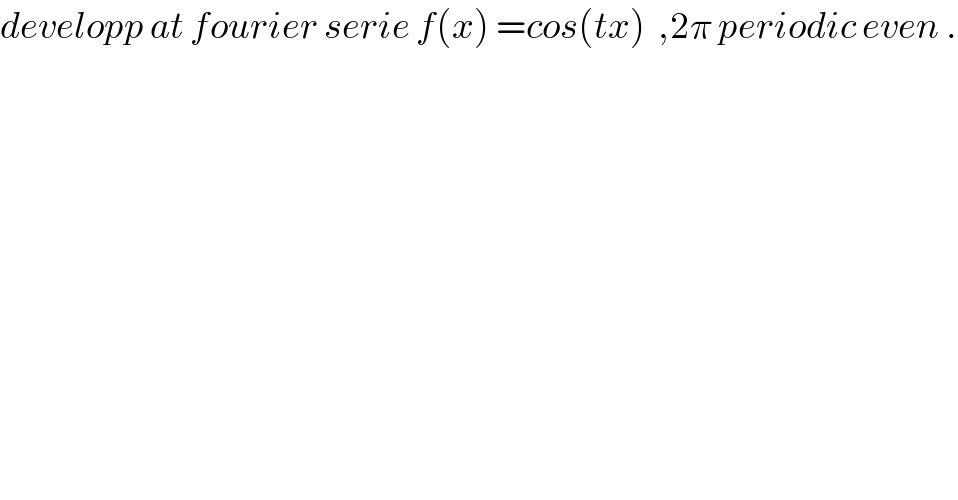
$${developp}\:{at}\:{fourier}\:{serie}\:{f}\left({x}\right)\:={cos}\left({tx}\right)\:\:,\mathrm{2}\pi\:{periodic}\:{even}\:. \\ $$
Commented by mathmax by abdo last updated on 28/Jun/19
![f is even ⇒f(x) =(a_0 /2) +Σ_(n=1) ^∞ a_n cos(nx) with a_n =(2/T) ∫_([T]) f(x)cos(nx)dx =(2/(2π)) ∫_(−π) ^π cos(tx)cos(nx)dx =(2/π) ∫_0 ^π cos(tx)cos(nx)dx =(1/π)∫_0 ^π { cos(t+n)x +cos(t−n)x}dx ⇒πa_n =[(1/(t+n)) sin(t+n)x+(1/(t−n))sin(t−n)x]_0 ^π =(1/(t+n))sin(tπ+nπ) +(1/(t−n)) sin(tπ−nπ) =(((−1)^n sin(πt))/(t+n)) +(((−1)^n sin(πt))/(t−n)) =(−1)^n sin(πt){(1/(t+n)) +(1/(t−n))} =(−1)^n sin(πt)((2t)/(t^2 −n^2 )) let find a_0 a_0 =(2/π) ∫_0 ^π cos(tx)dx =(2/π) [(1/t)sin(tx)]_0 ^π =(2/(πt)) sin(πt) ⇒ cos(tx) =((sin(πt))/(πt)) +Σ_(n=1) ^∞ (−1)^n ((2t sin(πt))/(π(t^2 −n^2 ))) cos(nx) ⇒ cos(tx) =((sin(πt))/(πt)) +((2t sin(πt))/π) Σ_(n=1) ^∞ (((−1)^n )/(t^2 −n^2 )) cos(nx) remark if we take x =π we get cos(πt) =((sin(πt))/(πt)) +((2t sin(πt))/π) Σ_(n=1) ^∞ (1/(t^2 −n^2 )) ⇒ cotan(πt) =(1/(πt)) +((2t)/π) Σ_(n=1) ^∞ (1/(t^2 −n^2 )) ⇒](https://www.tinkutara.com/question/Q63096.png)
$${f}\:{is}\:{even}\:\Rightarrow{f}\left({x}\right)\:=\frac{{a}_{\mathrm{0}} }{\mathrm{2}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:{a}_{{n}} \:{cos}\left({nx}\right)\:{with}\:{a}_{{n}} =\frac{\mathrm{2}}{{T}}\:\int_{\left[{T}\right]} \:\:{f}\left({x}\right){cos}\left({nx}\right){dx} \\ $$$$=\frac{\mathrm{2}}{\mathrm{2}\pi}\:\int_{−\pi} ^{\pi} \:{cos}\left({tx}\right){cos}\left({nx}\right){dx}\:=\frac{\mathrm{2}}{\pi}\:\int_{\mathrm{0}} ^{\pi} \:\:{cos}\left({tx}\right){cos}\left({nx}\right){dx}\: \\ $$$$=\frac{\mathrm{1}}{\pi}\int_{\mathrm{0}} ^{\pi} \left\{\:{cos}\left({t}+{n}\right){x}\:+{cos}\left({t}−{n}\right){x}\right\}{dx}\:\Rightarrow\pi{a}_{{n}} =\left[\frac{\mathrm{1}}{{t}+{n}}\:{sin}\left({t}+{n}\right){x}+\frac{\mathrm{1}}{{t}−{n}}{sin}\left({t}−{n}\right){x}\right]_{\mathrm{0}} ^{\pi} \\ $$$$=\frac{\mathrm{1}}{{t}+{n}}{sin}\left({t}\pi+{n}\pi\right)\:+\frac{\mathrm{1}}{{t}−{n}}\:{sin}\left({t}\pi−{n}\pi\right) \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}} {sin}\left(\pi{t}\right)}{{t}+{n}}\:+\frac{\left(−\mathrm{1}\right)^{{n}} \:{sin}\left(\pi{t}\right)}{{t}−{n}}\:=\left(−\mathrm{1}\right)^{{n}} \:{sin}\left(\pi{t}\right)\left\{\frac{\mathrm{1}}{{t}+{n}}\:+\frac{\mathrm{1}}{{t}−{n}}\right\} \\ $$$$=\left(−\mathrm{1}\right)^{{n}} {sin}\left(\pi{t}\right)\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} −{n}^{\mathrm{2}} }\:\:\:\:\:{let}\:{find}\:{a}_{\mathrm{0}} \\ $$$${a}_{\mathrm{0}} =\frac{\mathrm{2}}{\pi}\:\int_{\mathrm{0}} ^{\pi} \:{cos}\left({tx}\right){dx}\:=\frac{\mathrm{2}}{\pi}\:\left[\frac{\mathrm{1}}{{t}}{sin}\left({tx}\right)\right]_{\mathrm{0}} ^{\pi} \:=\frac{\mathrm{2}}{\pi{t}}\:{sin}\left(\pi{t}\right)\:\Rightarrow \\ $$$${cos}\left({tx}\right)\:=\frac{{sin}\left(\pi{t}\right)}{\pi{t}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{2}{t}\:{sin}\left(\pi{t}\right)}{\pi\left({t}^{\mathrm{2}} −{n}^{\mathrm{2}} \right)}\:{cos}\left({nx}\right)\:\Rightarrow \\ $$$${cos}\left({tx}\right)\:=\frac{{sin}\left(\pi{t}\right)}{\pi{t}}\:+\frac{\mathrm{2}{t}\:{sin}\left(\pi{t}\right)}{\pi}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{t}^{\mathrm{2}} −{n}^{\mathrm{2}} }\:{cos}\left({nx}\right) \\ $$$${remark}\:\:{if}\:{we}\:{take}\:{x}\:=\pi\:{we}\:{get}\: \\ $$$${cos}\left(\pi{t}\right)\:=\frac{{sin}\left(\pi{t}\right)}{\pi{t}}\:+\frac{\mathrm{2}{t}\:{sin}\left(\pi{t}\right)}{\pi}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{t}^{\mathrm{2}} −{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$${cotan}\left(\pi{t}\right)\:=\frac{\mathrm{1}}{\pi{t}}\:+\frac{\mathrm{2}{t}}{\pi}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{t}^{\mathrm{2}} −{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 03/Jul/19
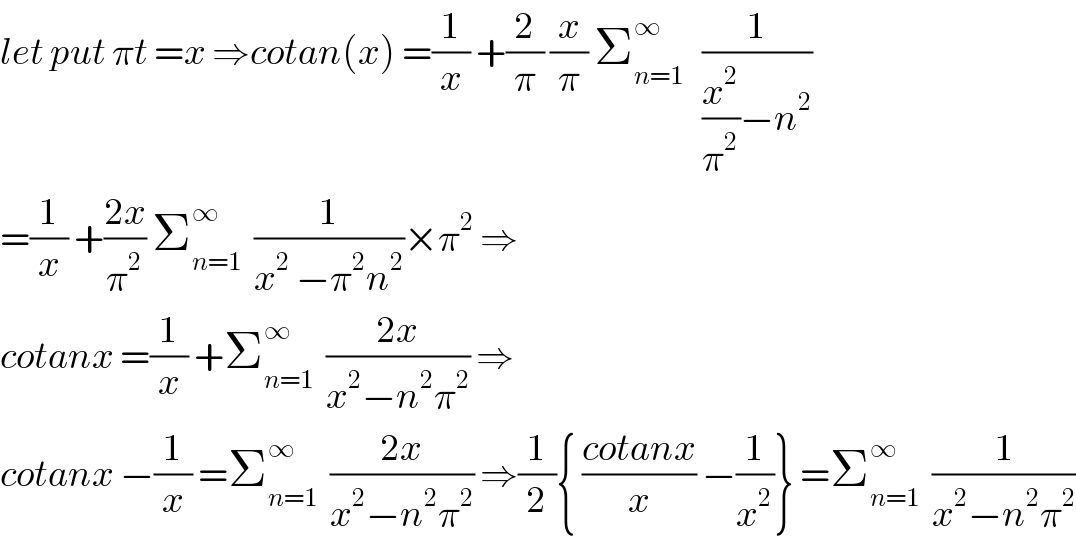
$${let}\:{put}\:\pi{t}\:={x}\:\Rightarrow{cotan}\left({x}\right)\:=\frac{\mathrm{1}}{{x}}\:+\frac{\mathrm{2}}{\pi}\:\frac{{x}}{\pi}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\frac{{x}^{\mathrm{2}} }{\pi^{\mathrm{2}} }−{n}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{{x}}\:+\frac{\mathrm{2}{x}}{\pi^{\mathrm{2}} }\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:−\pi^{\mathrm{2}} {n}^{\mathrm{2}} }×\pi^{\mathrm{2}} \:\Rightarrow \\ $$$${cotanx}\:=\frac{\mathrm{1}}{{x}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} −{n}^{\mathrm{2}} \pi^{\mathrm{2}} }\:\Rightarrow \\ $$$${cotanx}\:−\frac{\mathrm{1}}{{x}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} −{n}^{\mathrm{2}} \pi^{\mathrm{2}} }\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\frac{{cotanx}}{{x}}\:−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right\}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} −{n}^{\mathrm{2}} \pi^{\mathrm{2}} } \\ $$
