Menu Close

developp-at-integr-serie-f-x-0-x-sin-t-2-dt-

Tinku Tara 0 Comments
Pin




Question Number 33885 by math khazana by abdo last updated on 26/Apr/18
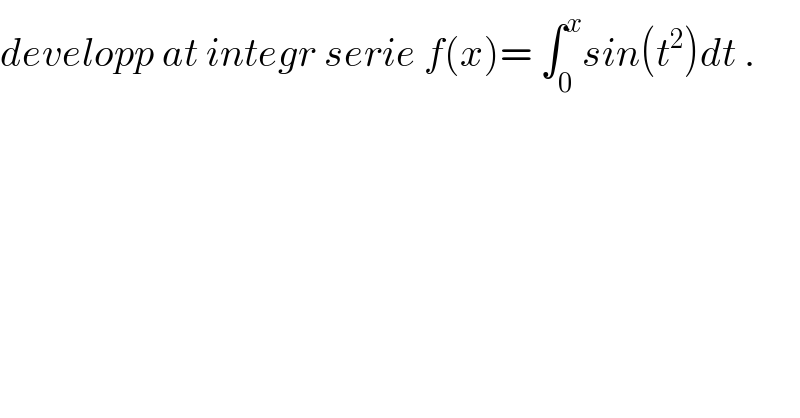
developp at integr serie f(x)= ∫_0 ^x sin(t^2 )dt .
developpatintegrserief(x)=∫0xsin(t2)dt.
Commented by prof Abdo imad last updated on 27/Apr/18
we know that sin(u) = Σ_(n=0) ^∞ (((−1)^n u^(2n+1) )/((2n+1)!)) let find the radius of convergence ∣(u_(n+1) /u_n )∣=(((2n+1)!)/((2n+3)!)) = (((2n+1)!)/((2n+3)(2n+2)(2n+1)!)) = (1/((2n+3)(2n+2))) →0 (n→+∞) so R=+∞ ⇒ sin(t^2 )= Σ_(n=0) ^∞ (((−1)^n t^(4n+2) )/((2n+1)!)) ⇒ f(x)=∫_0 ^x ( Σ_(n=0) ^∞ (((−1)^n )/((2n+1)!))t^(4n+2) )dt =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)!)) ∫_0 ^x t^(4n+2) dt f(x)= Σ_(n=0) ^∞ (((−1)^n )/((4n+3)(2n+1)!))x^(4n+3) .
weknowthatsin(u)=∑n=0∞(−1)nu2n+1(2n+1)!letfindtheradiusofconvergence∣un+1un∣=(2n+1)!(2n+3)!=(2n+1)!(2n+3)(2n+2)(2n+1)!=1(2n+3)(2n+2)→0(n→+∞)soR=+∞⇒sin(t2)=∑n=0∞(−1)nt4n+2(2n+1)!⇒f(x)=∫0x(∑n=0∞(−1)n(2n+1)!t4n+2)dt=∑n=0∞(−1)n(2n+1)!∫0xt4n+2dtf(x)=∑n=0∞(−1)n(4n+3)(2n+1)!x4n+3.

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *