Menu Close

developp-at-intergr-serie-f-x-1-x-3-x-2-4-

Tinku Tara 0 Comments
Pin




Question Number 94338 by mathmax by abdo last updated on 18/May/20
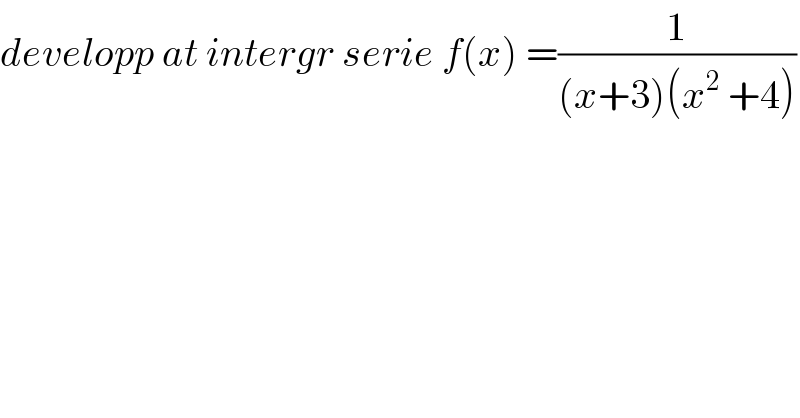
developp at intergr serie f(x) =(1/((x+3)(x^2 +4)))
$${developp}\:{at}\:{intergr}\:{serie}\:{f}\left({x}\right)\:=\frac{\mathrm{1}}{\left({x}+\mathrm{3}\right)\left({x}^{\mathrm{2}} \:+\mathrm{4}\right)} \\ $$
Answered by mathmax by abdo last updated on 18/May/20
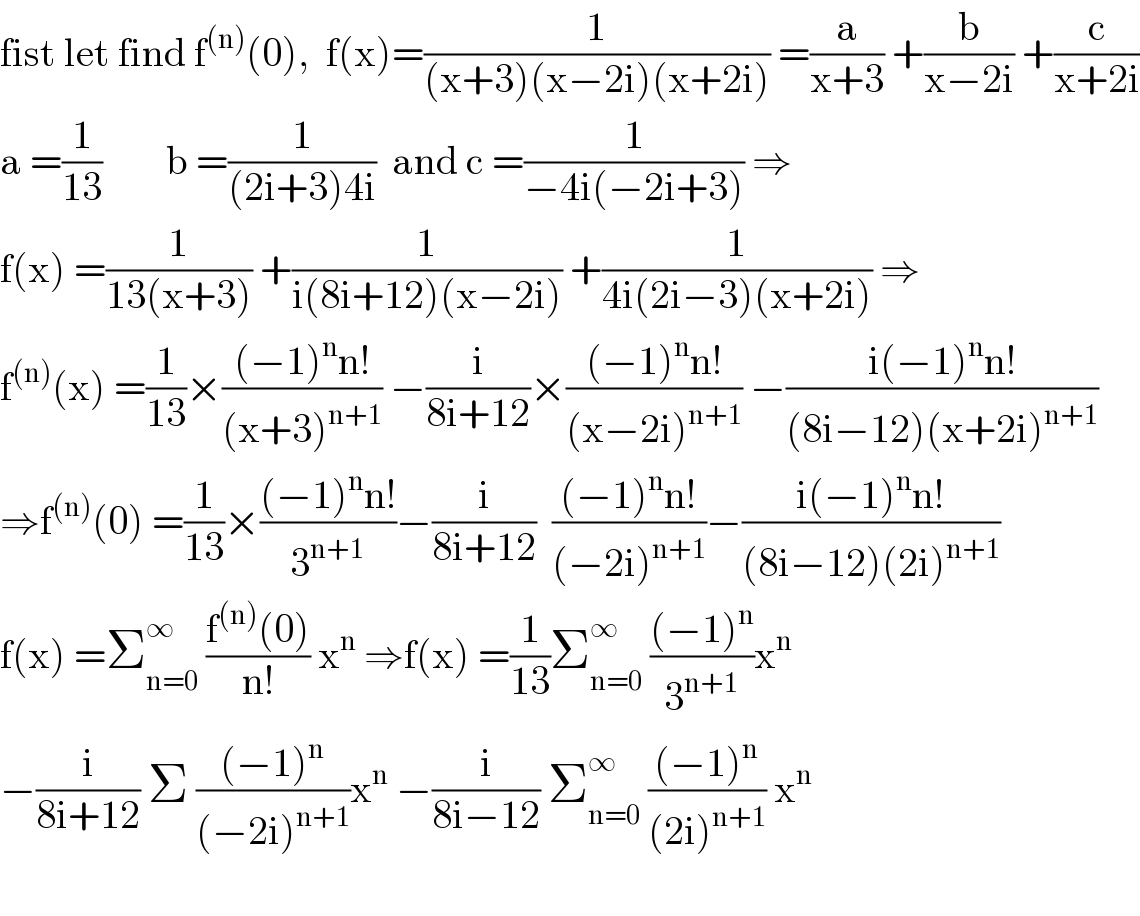
fist let find f^((n)) (0), f(x)=(1/((x+3)(x−2i)(x+2i))) =(a/(x+3)) +(b/(x−2i)) +(c/(x+2i)) a =(1/(13)) b =(1/((2i+3)4i)) and c =(1/(−4i(−2i+3))) ⇒ f(x) =(1/(13(x+3))) +(1/(i(8i+12)(x−2i))) +(1/(4i(2i−3)(x+2i))) ⇒ f^((n)) (x) =(1/(13))×(((−1)^n n!)/((x+3)^(n+1) )) −(i/(8i+12))×(((−1)^n n!)/((x−2i)^(n+1) )) −((i(−1)^n n!)/((8i−12)(x+2i)^(n+1) )) ⇒f^((n)) (0) =(1/(13))×(((−1)^n n!)/3^(n+1) )−(i/(8i+12)) (((−1)^n n!)/((−2i)^(n+1) ))−((i(−1)^n n!)/((8i−12)(2i)^(n+1) )) f(x) =Σ_(n=0) ^∞ ((f^((n)) (0))/(n!)) x^n ⇒f(x) =(1/(13))Σ_(n=0) ^∞ (((−1)^n )/3^(n+1) )x^n −(i/(8i+12)) Σ (((−1)^n )/((−2i)^(n+1) ))x^n −(i/(8i−12)) Σ_(n=0) ^∞ (((−1)^n )/((2i)^(n+1) )) x^n
$$\mathrm{fist}\:\mathrm{let}\:\mathrm{find}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right),\:\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{3}\right)\left(\mathrm{x}−\mathrm{2i}\right)\left(\mathrm{x}+\mathrm{2i}\right)}\:=\frac{\mathrm{a}}{\mathrm{x}+\mathrm{3}}\:+\frac{\mathrm{b}}{\mathrm{x}−\mathrm{2i}}\:+\frac{\mathrm{c}}{\mathrm{x}+\mathrm{2i}} \\ $$$$\mathrm{a}\:=\frac{\mathrm{1}}{\mathrm{13}}\:\:\:\:\:\:\:\:\mathrm{b}\:=\frac{\mathrm{1}}{\left(\mathrm{2i}+\mathrm{3}\right)\mathrm{4i}}\:\:\mathrm{and}\:\mathrm{c}\:=\frac{\mathrm{1}}{−\mathrm{4i}\left(−\mathrm{2i}+\mathrm{3}\right)}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{13}\left(\mathrm{x}+\mathrm{3}\right)}\:+\frac{\mathrm{1}}{\mathrm{i}\left(\mathrm{8i}+\mathrm{12}\right)\left(\mathrm{x}−\mathrm{2i}\right)}\:+\frac{\mathrm{1}}{\mathrm{4i}\left(\mathrm{2i}−\mathrm{3}\right)\left(\mathrm{x}+\mathrm{2i}\right)}\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{13}}×\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{n}!}{\left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{n}+\mathrm{1}} }\:−\frac{\mathrm{i}}{\mathrm{8i}+\mathrm{12}}×\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{n}!}{\left(\mathrm{x}−\mathrm{2i}\right)^{\mathrm{n}+\mathrm{1}} }\:−\frac{\mathrm{i}\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{n}!}{\left(\mathrm{8i}−\mathrm{12}\right)\left(\mathrm{x}+\mathrm{2i}\right)^{\mathrm{n}+\mathrm{1}} } \\ $$$$\Rightarrow\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)\:=\frac{\mathrm{1}}{\mathrm{13}}×\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{n}!}{\mathrm{3}^{\mathrm{n}+\mathrm{1}} }−\frac{\mathrm{i}}{\mathrm{8i}+\mathrm{12}}\:\:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{n}!}{\left(−\mathrm{2i}\right)^{\mathrm{n}+\mathrm{1}} }−\frac{\mathrm{i}\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{n}!}{\left(\mathrm{8i}−\mathrm{12}\right)\left(\mathrm{2i}\right)^{\mathrm{n}+\mathrm{1}} } \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)}{\mathrm{n}!}\:\mathrm{x}^{\mathrm{n}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{13}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{3}^{\mathrm{n}+\mathrm{1}} }\mathrm{x}^{\mathrm{n}} \\ $$$$−\frac{\mathrm{i}}{\mathrm{8i}+\mathrm{12}}\:\Sigma\:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(−\mathrm{2i}\right)^{\mathrm{n}+\mathrm{1}} }\mathrm{x}^{\mathrm{n}} \:−\frac{\mathrm{i}}{\mathrm{8i}−\mathrm{12}}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2i}\right)^{\mathrm{n}+\mathrm{1}} }\:\mathrm{x}^{\mathrm{n}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *