Menu Close

developp-at-laurent-series-1-f-z-1-z-2-2-g-z-3-z-2-3z-2-3-h-z-1-z-2-4-

Tinku Tara 0 Comments
Pin




Question Number 63560 by mathmax by abdo last updated on 05/Jul/19
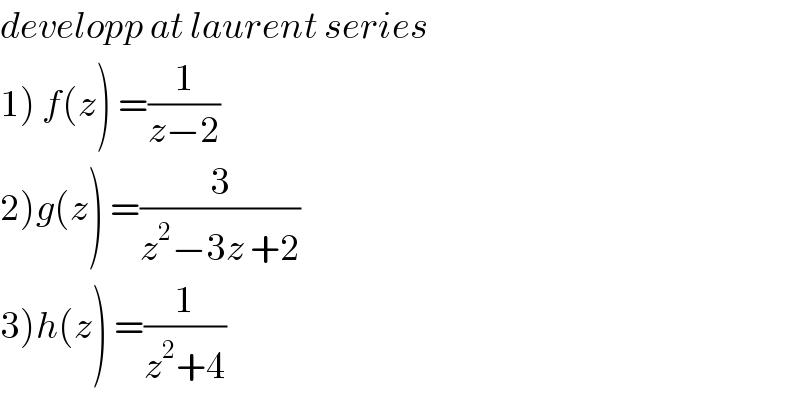
developp at laurent series 1) f(z) =(1/(z−2)) 2)g(z) =(3/(z^2 −3z +2)) 3)h(z) =(1/(z^2 +4))
$${developp}\:{at}\:{laurent}\:{series} \\ $$$$\left.\mathrm{1}\right)\:{f}\left({z}\right)\:=\frac{\mathrm{1}}{{z}−\mathrm{2}} \\ $$$$\left.\mathrm{2}\right){g}\left({z}\right)\:=\frac{\mathrm{3}}{{z}^{\mathrm{2}} −\mathrm{3}{z}\:+\mathrm{2}} \\ $$$$\left.\mathrm{3}\right){h}\left({z}\right)\:=\frac{\mathrm{1}}{{z}^{\mathrm{2}} +\mathrm{4}} \\ $$
Commented by mathmax by abdo last updated on 05/Jul/19
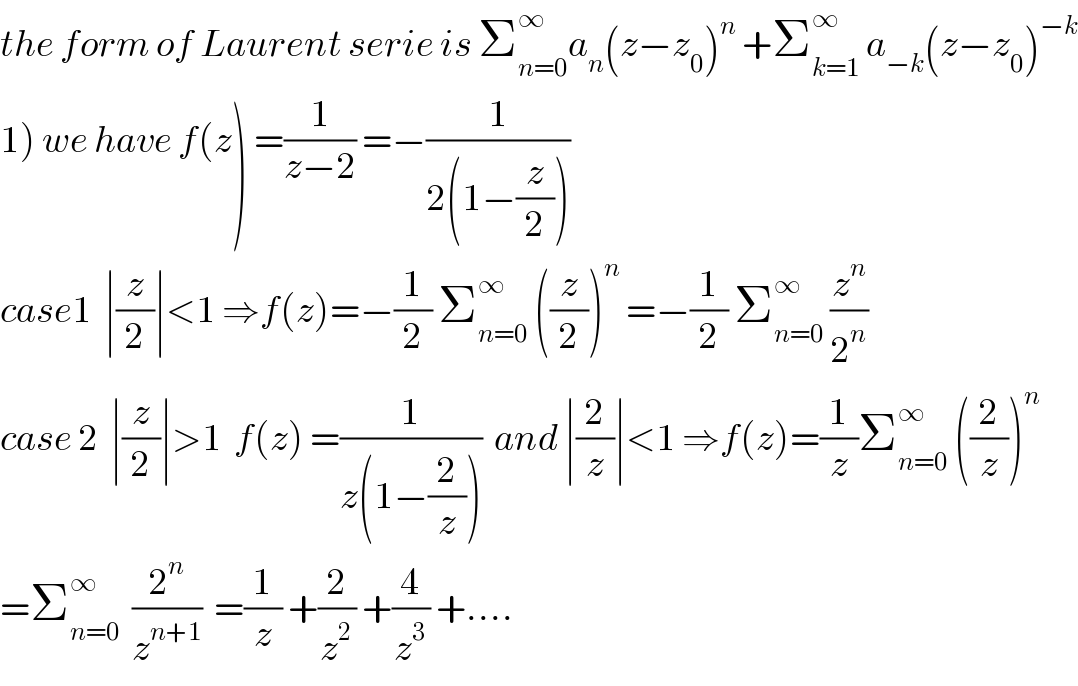
the form of Laurent serie is Σ_(n=0) ^∞ a_n (z−z_0 )^n +Σ_(k=1) ^∞ a_(−k) (z−z_0 )^(−k) 1) we have f(z) =(1/(z−2)) =−(1/(2(1−(z/2)))) case1 ∣(z/2)∣<1 ⇒f(z)=−(1/2) Σ_(n=0) ^∞ ((z/2))^n =−(1/2) Σ_(n=0) ^∞ (z^n /2^n ) case 2 ∣(z/2)∣>1 f(z) =(1/(z(1−(2/z)))) and ∣(2/z)∣<1 ⇒f(z)=(1/z)Σ_(n=0) ^∞ ((2/z))^n =Σ_(n=0) ^∞ (2^n /z^(n+1) ) =(1/z) +(2/z^2 ) +(4/z^3 ) +....
$${the}\:{form}\:{of}\:{Laurent}\:{serie}\:{is}\:\sum_{{n}=\mathrm{0}} ^{\infty} {a}_{{n}} \left({z}−{z}_{\mathrm{0}} \right)^{{n}} \:+\sum_{{k}=\mathrm{1}} ^{\infty} \:{a}_{−{k}} \left({z}−{z}_{\mathrm{0}} \right)^{−{k}} \\ $$$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({z}\right)\:=\frac{\mathrm{1}}{{z}−\mathrm{2}}\:=−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\frac{{z}}{\mathrm{2}}\right)} \\ $$$${case}\mathrm{1}\:\:\mid\frac{{z}}{\mathrm{2}}\mid<\mathrm{1}\:\Rightarrow{f}\left({z}\right)=−\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(\frac{{z}}{\mathrm{2}}\right)^{{n}} \:=−\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{z}^{{n}} }{\mathrm{2}^{{n}} } \\ $$$${case}\:\mathrm{2}\:\:\mid\frac{{z}}{\mathrm{2}}\mid>\mathrm{1}\:\:{f}\left({z}\right)\:=\frac{\mathrm{1}}{{z}\left(\mathrm{1}−\frac{\mathrm{2}}{{z}}\right)}\:\:{and}\:\mid\frac{\mathrm{2}}{{z}}\mid<\mathrm{1}\:\Rightarrow{f}\left({z}\right)=\frac{\mathrm{1}}{{z}}\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(\frac{\mathrm{2}}{{z}}\right)^{{n}} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}^{{n}} }{{z}^{{n}+\mathrm{1}} }\:\:=\frac{\mathrm{1}}{{z}}\:+\frac{\mathrm{2}}{{z}^{\mathrm{2}} }\:+\frac{\mathrm{4}}{{z}^{\mathrm{3}} }\:+…. \\ $$
Commented by mathmax by abdo last updated on 10/Jul/19
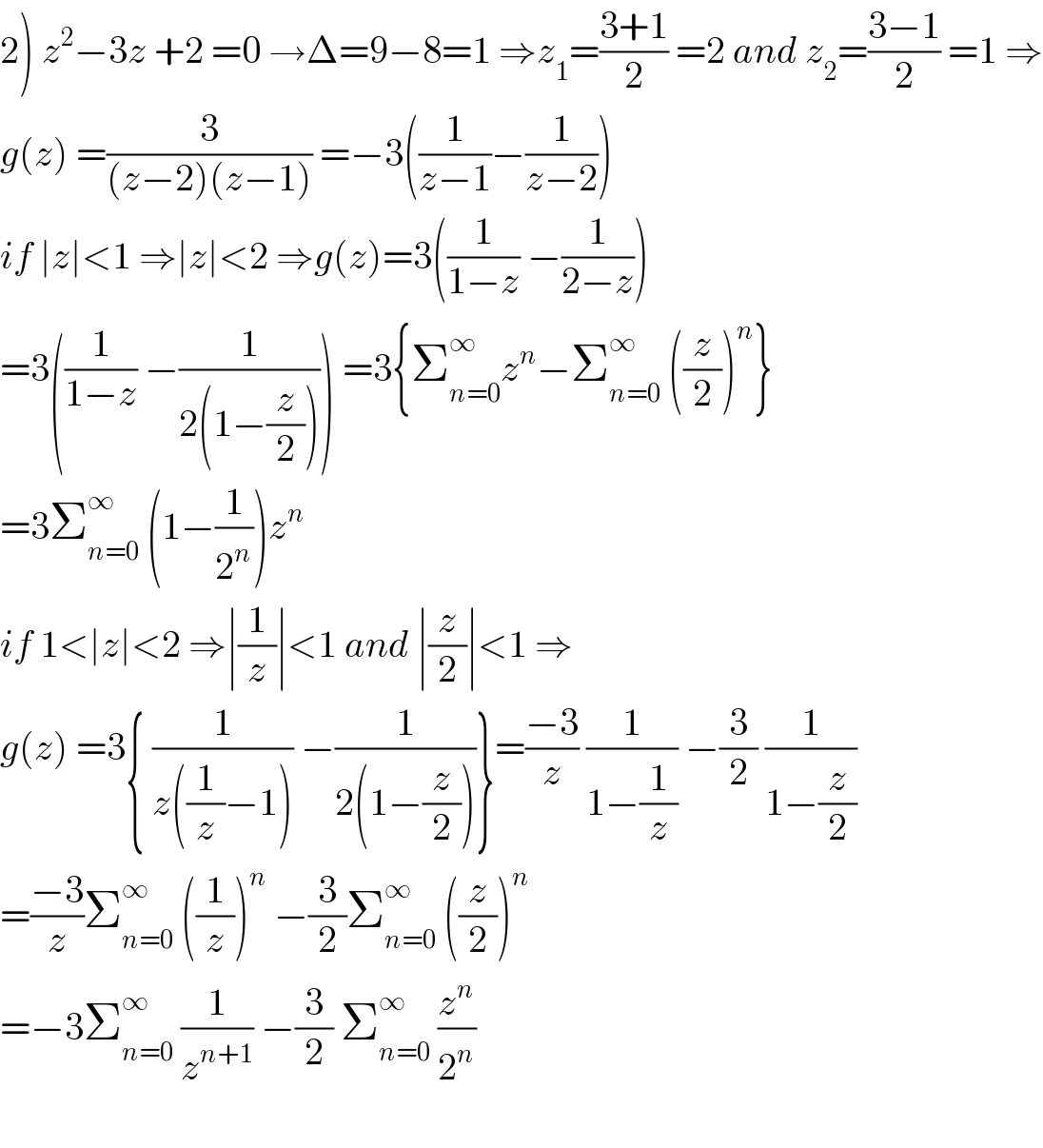
2) z^2 −3z +2 =0 →Δ=9−8=1 ⇒z_1 =((3+1)/2) =2 and z_2 =((3−1)/2) =1 ⇒ g(z) =(3/((z−2)(z−1))) =−3((1/(z−1))−(1/(z−2))) if ∣z∣<1 ⇒∣z∣<2 ⇒g(z)=3((1/(1−z)) −(1/(2−z))) =3((1/(1−z)) −(1/(2(1−(z/2))))) =3{Σ_(n=0) ^∞ z^n −Σ_(n=0) ^∞ ((z/2))^n } =3Σ_(n=0) ^∞ (1−(1/2^n ))z^n if 1<∣z∣<2 ⇒∣(1/z)∣<1 and ∣(z/2)∣<1 ⇒ g(z) =3{ (1/(z((1/z)−1))) −(1/(2(1−(z/2))))}=((−3)/z) (1/(1−(1/z))) −(3/2) (1/(1−(z/2))) =((−3)/z)Σ_(n=0) ^∞ ((1/z))^n −(3/2)Σ_(n=0) ^∞ ((z/2))^n =−3Σ_(n=0) ^∞ (1/z^(n+1) ) −(3/2) Σ_(n=0) ^∞ (z^n /2^n )
$$\left.\mathrm{2}\right)\:{z}^{\mathrm{2}} −\mathrm{3}{z}\:+\mathrm{2}\:=\mathrm{0}\:\rightarrow\Delta=\mathrm{9}−\mathrm{8}=\mathrm{1}\:\Rightarrow{z}_{\mathrm{1}} =\frac{\mathrm{3}+\mathrm{1}}{\mathrm{2}}\:=\mathrm{2}\:{and}\:{z}_{\mathrm{2}} =\frac{\mathrm{3}−\mathrm{1}}{\mathrm{2}}\:=\mathrm{1}\:\Rightarrow \\ $$$${g}\left({z}\right)\:=\frac{\mathrm{3}}{\left({z}−\mathrm{2}\right)\left({z}−\mathrm{1}\right)}\:=−\mathrm{3}\left(\frac{\mathrm{1}}{{z}−\mathrm{1}}−\frac{\mathrm{1}}{{z}−\mathrm{2}}\right) \\ $$$${if}\:\mid{z}\mid<\mathrm{1}\:\Rightarrow\mid{z}\mid<\mathrm{2}\:\Rightarrow{g}\left({z}\right)=\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{1}−{z}}\:−\frac{\mathrm{1}}{\mathrm{2}−{z}}\right) \\ $$$$=\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{1}−{z}}\:−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\frac{{z}}{\mathrm{2}}\right)}\right)\:=\mathrm{3}\left\{\sum_{{n}=\mathrm{0}} ^{\infty} {z}^{{n}} −\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(\frac{{z}}{\mathrm{2}}\right)^{{n}} \right\} \\ $$$$=\mathrm{3}\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right){z}^{{n}} \\ $$$${if}\:\mathrm{1}<\mid{z}\mid<\mathrm{2}\:\Rightarrow\mid\frac{\mathrm{1}}{{z}}\mid<\mathrm{1}\:{and}\:\mid\frac{{z}}{\mathrm{2}}\mid<\mathrm{1}\:\Rightarrow \\ $$$${g}\left({z}\right)\:=\mathrm{3}\left\{\:\frac{\mathrm{1}}{{z}\left(\frac{\mathrm{1}}{{z}}−\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\frac{{z}}{\mathrm{2}}\right)}\right\}=\frac{−\mathrm{3}}{{z}}\:\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{{z}}}\:−\frac{\mathrm{3}}{\mathrm{2}}\:\frac{\mathrm{1}}{\mathrm{1}−\frac{{z}}{\mathrm{2}}} \\ $$$$=\frac{−\mathrm{3}}{{z}}\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(\frac{\mathrm{1}}{{z}}\right)^{{n}} \:−\frac{\mathrm{3}}{\mathrm{2}}\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(\frac{{z}}{\mathrm{2}}\right)^{{n}} \\ $$$$=−\mathrm{3}\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{z}^{{n}+\mathrm{1}} }\:−\frac{\mathrm{3}}{\mathrm{2}}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{z}^{{n}} }{\mathrm{2}^{{n}} } \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *