Question Number 127152 by mnjuly1970 last updated on 27/Dec/20
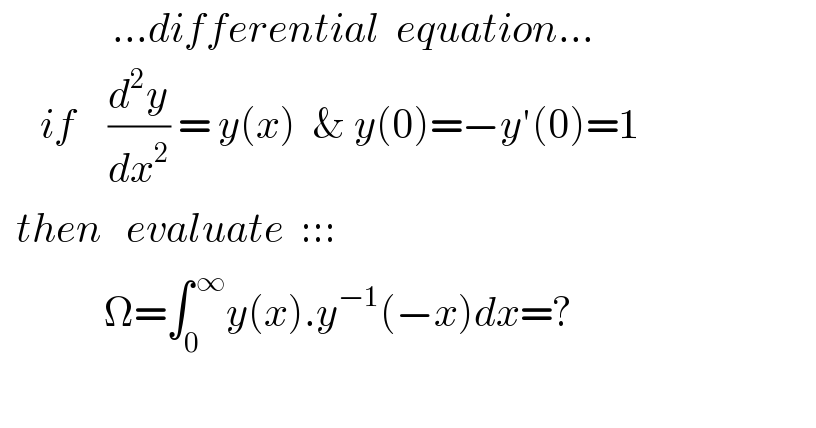
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:…{differential}\:\:{equation}…\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:{if}\:\:\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\:{y}\left({x}\right)\:\:\&\:{y}\left(\mathrm{0}\right)=−{y}'\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$\:\:{then}\:\:\:{evaluate}\:\:::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\infty} {y}\left({x}\right).{y}^{−\mathrm{1}} \left(−{x}\right){dx}=? \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 27/Dec/20
![y^(′′) =y and y(0)=1 ,y^′ (0)=−1 r^2 −1=0 ⇒y =ae^x +be^(−x) y(0)=1 ⇒a+b=1 ,y^′ =ae^x −be^(−x) ,y^′ (0)=−1 ⇒a−b=−1 ⇒ { ((a+b=1)),((a−b=−1 ⇒ { ((a=0 ⇒y(x)=e^(−x) )),((b=1 )) :})) :} y(x)=t ⇒x=y^(−1) (t) ⇒e^(−x) =t ⇒−x =ln(t) ⇒x=−lnt ⇒ y^(−1) (x)=−lnx ⇒Ω =∫_0 ^∞ e^(−x) (−ln(−x))dx =−∫_0 ^∞ e^(−x) (iπ +ln(x))dx =−iπ ∫_0 ^∞ e^(−x) dx −∫_0 ^∞ e^(−x) ln(x)dx =−iπ[−e^(−x) ]_0 ^∞ +γ =γ−iπ](https://www.tinkutara.com/question/Q127162.png)
$$\mathrm{y}^{''} =\mathrm{y}\:\:\mathrm{and}\:\mathrm{y}\left(\mathrm{0}\right)=\mathrm{1}\:,\mathrm{y}^{'} \left(\mathrm{0}\right)=−\mathrm{1} \\ $$$$\mathrm{r}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\:\Rightarrow\mathrm{y}\:=\mathrm{ae}^{\mathrm{x}} \:+\mathrm{be}^{−\mathrm{x}} \\ $$$$\mathrm{y}\left(\mathrm{0}\right)=\mathrm{1}\:\Rightarrow\mathrm{a}+\mathrm{b}=\mathrm{1}\:,\mathrm{y}^{'} \:=\mathrm{ae}^{\mathrm{x}} −\mathrm{be}^{−\mathrm{x}} \:,\mathrm{y}^{'} \left(\mathrm{0}\right)=−\mathrm{1}\:\Rightarrow\mathrm{a}−\mathrm{b}=−\mathrm{1}\:\Rightarrow \\ $$$$\begin{cases}{\mathrm{a}+\mathrm{b}=\mathrm{1}}\\{\mathrm{a}−\mathrm{b}=−\mathrm{1}\:\:\Rightarrow\begin{cases}{\mathrm{a}=\mathrm{0}\:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)=\mathrm{e}^{−\mathrm{x}} }\\{\mathrm{b}=\mathrm{1}\:\:}\end{cases}}\end{cases} \\ $$$$\mathrm{y}\left(\mathrm{x}\right)=\mathrm{t}\:\Rightarrow\mathrm{x}=\mathrm{y}^{−\mathrm{1}} \left(\mathrm{t}\right)\:\Rightarrow\mathrm{e}^{−\mathrm{x}} \:=\mathrm{t}\:\Rightarrow−\mathrm{x}\:=\mathrm{ln}\left(\mathrm{t}\right)\:\Rightarrow\mathrm{x}=−\mathrm{lnt}\:\Rightarrow \\ $$$$\mathrm{y}^{−\mathrm{1}} \left(\mathrm{x}\right)=−\mathrm{lnx}\:\Rightarrow\Omega\:=\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{x}} \:\left(−\mathrm{ln}\left(−\mathrm{x}\right)\right)\mathrm{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}} \left(\mathrm{i}\pi\:+\mathrm{ln}\left(\mathrm{x}\right)\right)\mathrm{dx}\:\:=−\mathrm{i}\pi\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}} \mathrm{dx}\:−\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$=−\mathrm{i}\pi\left[−\mathrm{e}^{−\mathrm{x}} \right]_{\mathrm{0}} ^{\infty} +\gamma\:\:=\gamma−\mathrm{i}\pi \\ $$
Commented by mnjuly1970 last updated on 27/Dec/20
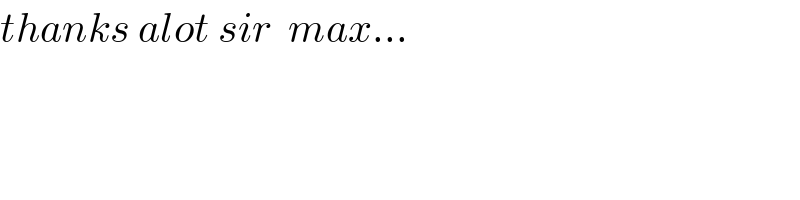
$${thanks}\:{alot}\:{sir}\:\:{max}… \\ $$
Commented by mathmax by abdo last updated on 27/Dec/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
Answered by mnjuly1970 last updated on 27/Dec/20
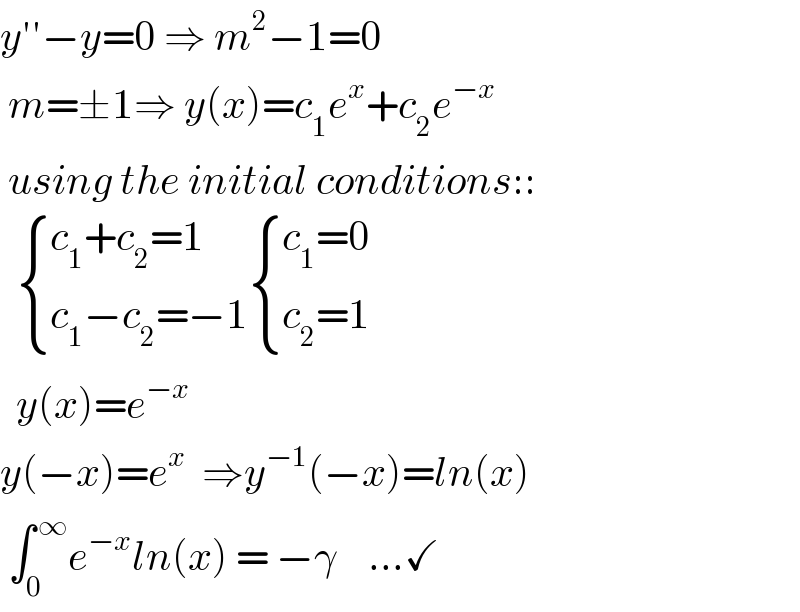
$${y}''−{y}=\mathrm{0}\:\Rightarrow\:{m}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\:{m}=\pm\mathrm{1}\Rightarrow\:{y}\left({x}\right)={c}_{\mathrm{1}} {e}^{{x}} +{c}_{\mathrm{2}} {e}^{−{x}} \\ $$$$\:{using}\:{the}\:{initial}\:{conditions}:: \\ $$$$\:\:\begin{cases}{{c}_{\mathrm{1}} +{c}_{\mathrm{2}} =\mathrm{1}}\\{{c}_{\mathrm{1}} −{c}_{\mathrm{2}} =−\mathrm{1}}\end{cases}\begin{cases}{{c}_{\mathrm{1}} =\mathrm{0}}\\{{c}_{\mathrm{2}} =\mathrm{1}}\end{cases} \\ $$$$\:\:{y}\left({x}\right)={e}^{−{x}} \\ $$$${y}\left(−{x}\right)={e}^{{x}} \:\:\Rightarrow{y}^{−\mathrm{1}} \left(−{x}\right)={ln}\left({x}\right) \\ $$$$\:\int_{\mathrm{0}\:} ^{\:\infty} {e}^{−{x}} {ln}\left({x}\right)\:=\:−\gamma\:\:\:\:…\checkmark \\ $$
Answered by Dwaipayan Shikari last updated on 27/Dec/20
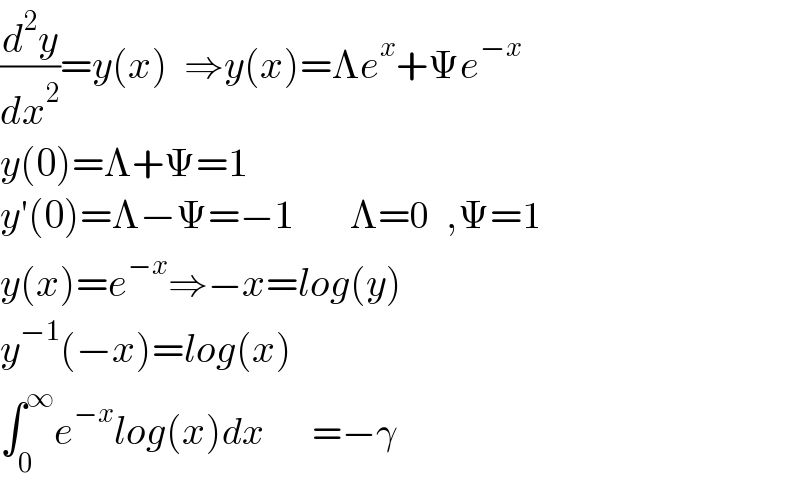
$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }={y}\left({x}\right)\:\:\Rightarrow{y}\left({x}\right)=\Lambda{e}^{{x}} +\Psi{e}^{−{x}} \\ $$$${y}\left(\mathrm{0}\right)=\Lambda+\Psi=\mathrm{1} \\ $$$${y}'\left(\mathrm{0}\right)=\Lambda−\Psi=−\mathrm{1}\:\:\:\:\:\:\:\Lambda=\mathrm{0}\:\:,\Psi=\mathrm{1} \\ $$$${y}\left({x}\right)={e}^{−{x}} \Rightarrow−{x}={log}\left({y}\right) \\ $$$${y}^{−\mathrm{1}} \left(−{x}\right)={log}\left({x}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} {log}\left({x}\right){dx}\:\:\:\:\:\:=−\gamma \\ $$
Commented by mnjuly1970 last updated on 27/Dec/20

$${grateful}… \\ $$
