Differentiate-the-following-wrt-x-1-y-x-x-2-y-sin-1-2x-1-Mastermind-

Question Number 169305 by Mastermind last updated on 28/Apr/22

$${Differentiate}\:{the}\:{following}\:{wrt}\:{x} \\ $$$$\left.\mathrm{1}\right)\:{y}={x}^{{x}} \\ $$$$\left.\mathrm{2}\right)\:{y}={sin}^{−\mathrm{1}} \left(\mathrm{2}{x}+\mathrm{1}\right) \\ $$$$ \\ $$$${Mastermind} \\ $$

Commented by infinityaction last updated on 28/Apr/22

$$\mathrm{log}\:{y}\:\:=\:\:\:{x}\mathrm{log}\:{x} \\ $$$$\frac{\mathrm{1}}{{y}}\frac{{dy}}{{dx}}\:\:=\:\mathrm{1}+\mathrm{log}\:{x} \\ $$$$\frac{{dy}}{{dx}}\:\:\:=\:\:\:{x}^{{x}} \left\{\mathrm{1}+\mathrm{log}\:\mid{x}\mid\right\} \\ $$

Commented by Mastermind last updated on 29/Apr/22

$${what}\:{of}\:{no}.\:\mathrm{2}? \\ $$

Answered by rexford last updated on 28/Apr/22

$$\left(\mathrm{1}\right)\:{lny}={xlnx} \\ $$$$\frac{{y}'}{{y}}={lnx}+\mathrm{1} \\ $$$${y}'={y}\left[{lnx}+\mathrm{1}\right] \\ $$$${y}'={x}^{{x}} \left[{lnx}+\mathrm{1}\right] \\ $$

Answered by rexford last updated on 28/Apr/22

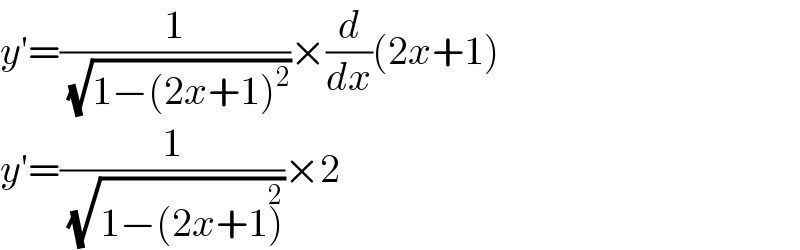
$${y}'=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} }}×\frac{{d}}{{dx}}\left(\mathrm{2}{x}+\mathrm{1}\right) \\ $$$${y}'=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\left(\mathrm{2}{x}+\mathrm{1}\overset{\mathrm{2}} {\right)}}}×\mathrm{2} \\ $$

Commented by infinityaction last updated on 29/Apr/22

$${x}\:=\:\left(−\mathrm{1},\mathrm{0}\right) \\ $$

Answered by thfchristopher last updated on 30/Apr/22

$$\left.\mathrm{1}\right)\:{y}={x}^{{x}} \\ $$$$\Rightarrow\mathrm{ln}\:{y}={x}\mathrm{ln}\:{x} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{y}}\frac{{dy}}{{dx}}=\frac{{x}}{{x}}+\mathrm{ln}\:{x} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}={y}\left(\mathrm{1}+\mathrm{ln}\:{x}\right) \\ $$$$={x}^{{x}} \left(\mathrm{1}+\mathrm{ln}\:{x}\right) \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\:{y}=\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{2}{x}+\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{sin}\:{y}=\mathrm{2}{x}+\mathrm{1} \\ $$$$\Rightarrow\mathrm{cos}\:{y}\frac{{dy}}{{dx}}=\mathrm{2} \\ $$$$\Rightarrow\sqrt{\mathrm{1}−\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} }\frac{{dy}}{{dx}}=\mathrm{2} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} }} \\ $$

Answered by MikeH last updated on 01/May/22

$$\mathrm{ln}\:{y}\:=\:{x}\:\mathrm{ln}\:{x} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{{y}}\:\frac{{dy}}{{dx}}\:=\:\mathrm{ln}\:{x}\:+\:{x}\left(\frac{\mathrm{1}}{{x}}\right) \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}}\:=\:{y}\left(\mathrm{ln}\:{x}\:+\mathrm{1}\right) \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}\:}\:=\:{x}^{{x}} \left(\mathrm{ln}\:{x}\:+\:\mathrm{1}\right) \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com