Question Number 169612 by Mastermind last updated on 04/May/22
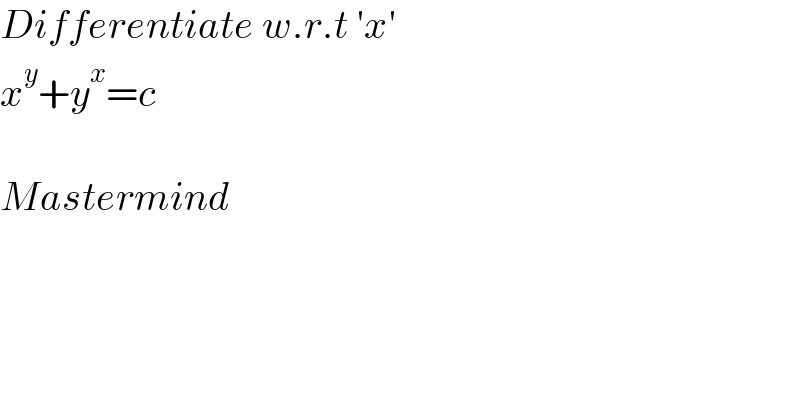
$${Differentiate}\:{w}.{r}.{t}\:'{x}'\: \\ $$$${x}^{{y}} +{y}^{{x}} ={c} \\ $$$$ \\ $$$${Mastermind} \\ $$
Answered by thfchristopher last updated on 04/May/22
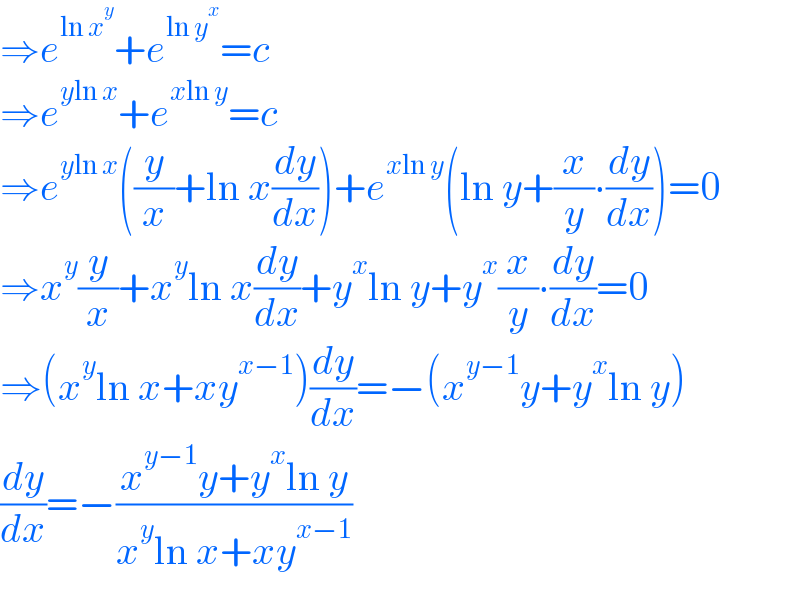
$$\Rightarrow{e}^{\mathrm{ln}\:{x}^{{y}} } +{e}^{\mathrm{ln}\:{y}^{{x}} } ={c} \\ $$$$\Rightarrow{e}^{{y}\mathrm{ln}\:{x}} +{e}^{{x}\mathrm{ln}\:{y}} ={c} \\ $$$$\Rightarrow{e}^{{y}\mathrm{ln}\:{x}} \left(\frac{{y}}{{x}}+\mathrm{ln}\:{x}\frac{{dy}}{{dx}}\right)+{e}^{{x}\mathrm{ln}\:{y}} \left(\mathrm{ln}\:{y}+\frac{{x}}{{y}}\centerdot\frac{{dy}}{{dx}}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}^{{y}} \frac{{y}}{{x}}+{x}^{{y}} \mathrm{ln}\:{x}\frac{{dy}}{{dx}}+{y}^{{x}} \mathrm{ln}\:{y}+{y}^{{x}} \frac{{x}}{{y}}\centerdot\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\Rightarrow\left({x}^{{y}} \mathrm{ln}\:{x}+{xy}^{{x}−\mathrm{1}} \right)\frac{{dy}}{{dx}}=−\left({x}^{{y}−\mathrm{1}} {y}+{y}^{{x}} \mathrm{ln}\:{y}\right) \\ $$$$\frac{{dy}}{{dx}}=−\frac{{x}^{{y}−\mathrm{1}} {y}+{y}^{{x}} \mathrm{ln}\:{y}}{{x}^{{y}} \mathrm{ln}\:{x}+{xy}^{{x}−\mathrm{1}} } \\ $$
Commented by Mastermind last updated on 04/May/22

$${Thanks} \\ $$
