Question Number 169347 by Mastermind last updated on 29/Apr/22
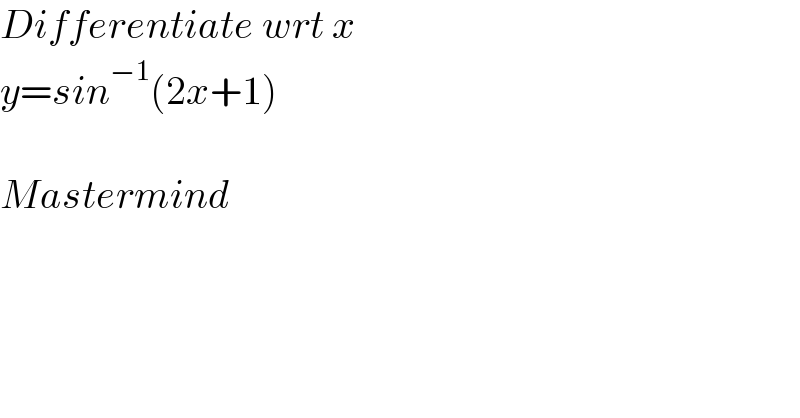
$${Differentiate}\:{wrt}\:{x} \\ $$$${y}={sin}^{−\mathrm{1}} \left(\mathrm{2}{x}+\mathrm{1}\right) \\ $$$$ \\ $$$${Mastermind} \\ $$
Answered by Mathspace last updated on 29/Apr/22
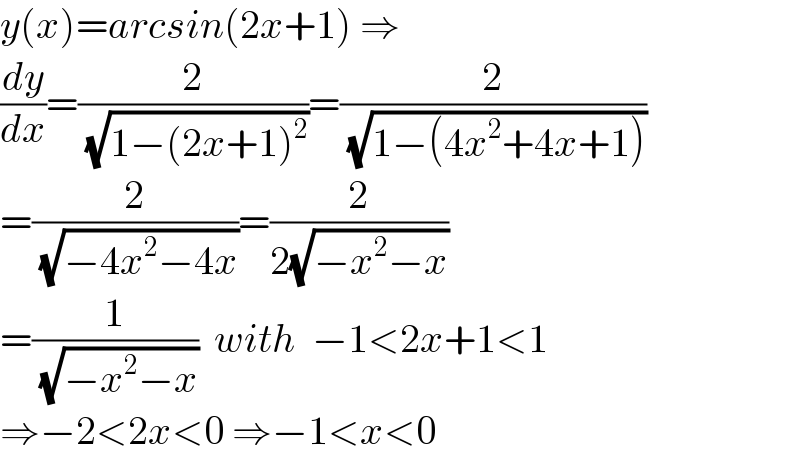
$${y}\left({x}\right)={arcsin}\left(\mathrm{2}{x}+\mathrm{1}\right)\:\Rightarrow \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} }}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{1}\right)}} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{−\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}}}=\frac{\mathrm{2}}{\mathrm{2}\sqrt{−{x}^{\mathrm{2}} −{x}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{−{x}^{\mathrm{2}} −{x}}}\:\:{with}\:\:−\mathrm{1}<\mathrm{2}{x}+\mathrm{1}<\mathrm{1} \\ $$$$\Rightarrow−\mathrm{2}<\mathrm{2}{x}<\mathrm{0}\:\Rightarrow−\mathrm{1}<{x}<\mathrm{0} \\ $$
Answered by alephzero last updated on 29/Apr/22
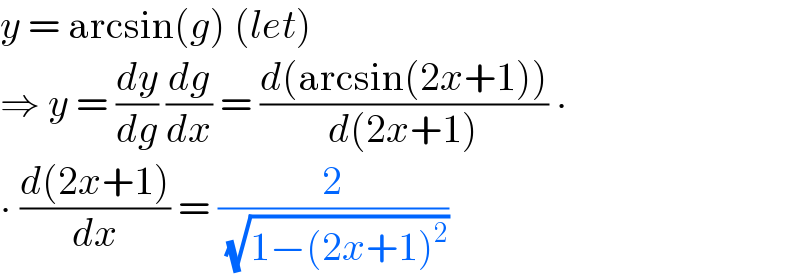
$${y}\:=\:\mathrm{arcsin}\left({g}\right)\:\left({let}\right) \\ $$$$\Rightarrow\:{y}\:=\:\frac{{dy}}{{dg}}\:\frac{{dg}}{{dx}}\:=\:\frac{{d}\left(\mathrm{arcsin}\left(\mathrm{2}{x}+\mathrm{1}\right)\right)}{{d}\left(\mathrm{2}{x}+\mathrm{1}\right)}\:\centerdot \\ $$$$\centerdot\:\frac{{d}\left(\mathrm{2}{x}+\mathrm{1}\right)}{{dx}}\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} }} \\ $$
Answered by thfchristopher last updated on 29/Apr/22
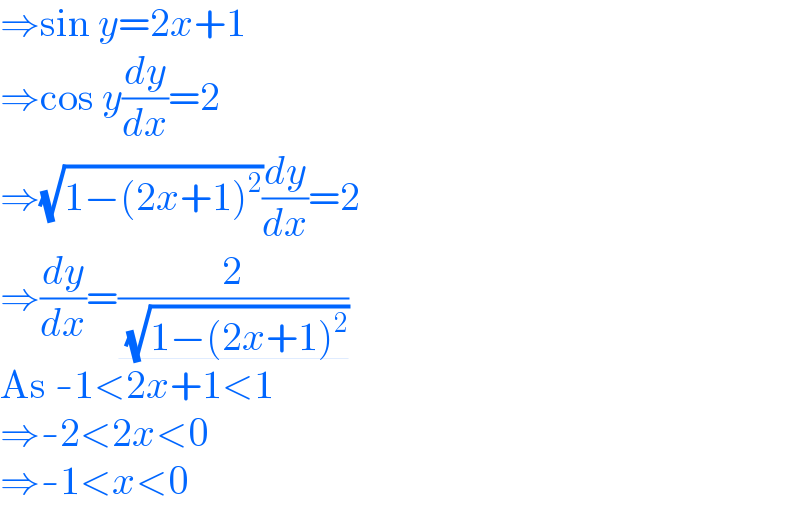
$$\Rightarrow\mathrm{sin}\:{y}=\mathrm{2}{x}+\mathrm{1} \\ $$$$\Rightarrow\mathrm{cos}\:{y}\frac{{dy}}{{dx}}=\mathrm{2} \\ $$$$\Rightarrow\sqrt{\mathrm{1}−\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} }\frac{{dy}}{{dx}}=\mathrm{2} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}=\underline{\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} }}} \\ $$$$\mathrm{As}\:-\mathrm{1}<\mathrm{2}{x}+\mathrm{1}<\mathrm{1} \\ $$$$\Rightarrow-\mathrm{2}<\mathrm{2}{x}<\mathrm{0} \\ $$$$\Rightarrow-\mathrm{1}<{x}<\mathrm{0} \\ $$
Answered by peter frank last updated on 29/Apr/22

$$\mathrm{u}=\mathrm{2x}+\mathrm{1} \\ $$$$\mathrm{y}=\mathrm{sin}^{−\mathrm{1}} \mathrm{u} \\ $$$$\mathrm{then}\:\mathrm{apply}\:\mathrm{chain}\:\mathrm{rule} \\ $$
