Differentiate-y-2-x-from-the-first-principle-

Question Number 82018 by TawaTawa last updated on 17/Feb/20

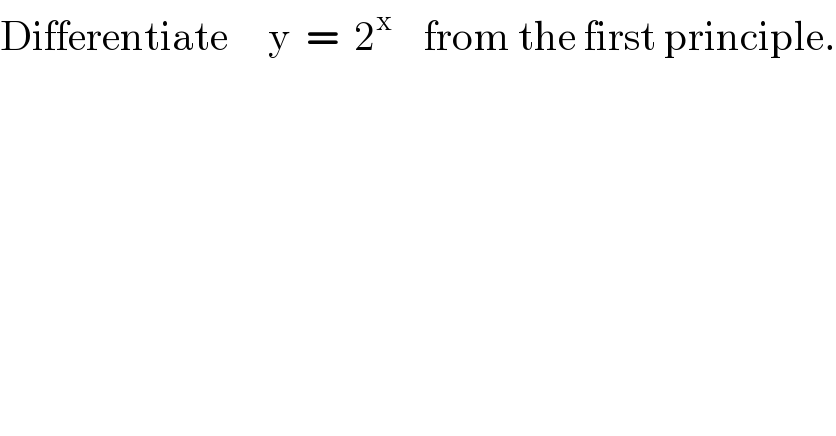
Differentiate y = 2^{x} from the first principle .

Commented by john santu last updated on 17/Feb/20

l n y = x l n 2

\lim_{h \to 0} l n (y) = \lim_{h \to 0} l n (2) \frac{(x + h) - x}{h}

\frac{y^{'}}{y} = l n (2) \lim_{h \to 0} \frac{h}{h}

y^{'} = y . l n (2) = 2^{x} . l n (2)

Commented by TawaTawa last updated on 17/Feb/20

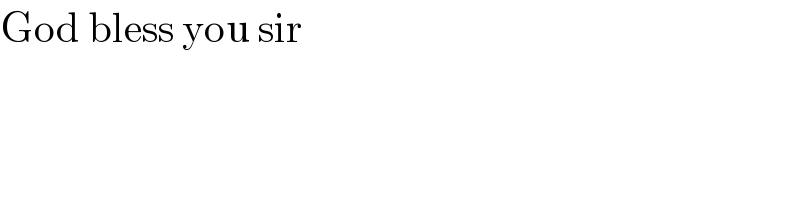
God bless you sir

Answered by TANMAY PANACEA last updated on 17/Feb/20

y + △ y = 2^{x + △ x}

△ y = 2^{x + △ x} - 2^{x} = 2^{x} (2^{△ x} - 1)

\frac{d y}{d x} = \lim_{△ x \to 0} \frac{△ y}{△ x} =

= \lim_{△ x \to 0} \frac{2^{x} (2^{△ x} - 1)}{△ x}

= 2^{x} \times (\lim_{△ x \to 0} \frac{e^{△ x . l n 2} - 1}{△ x . l n 2}) \times l n 2

= 2^{x} \times 1 \times l n 2 = 2^{x} l n 2

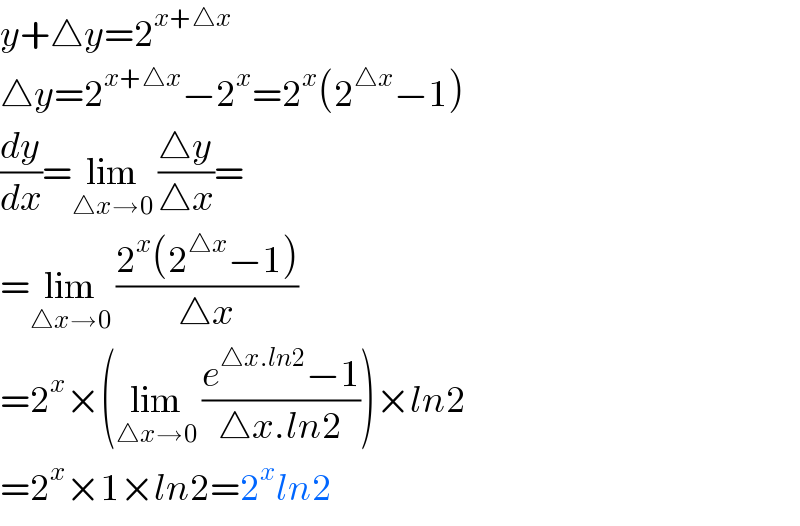
Commented by TawaTawa last updated on 17/Feb/20

God bless you sir

Answered by mr W last updated on 17/Feb/20

y^{'} = \lim_{h \to 0} \frac{2^{x + h} - 2^{x}}{h}

= 2^{x} \lim_{h \to 0} \frac{2^{h} - 1}{h}

= 2^{x} \lim_{h \to 0} \frac{e^{h \ln 2} - 1}{h}

= 2^{x} \lim_{h \to 0} \frac{[1 + h \ln 2 + \frac{{(h \ln 2)}^{2}}{2!} + \frac{{(h \ln 2)}^{3}}{3!} + \dots] - 1}{h}

= 2^{x} \lim_{h \to 0} [\ln 2 + \frac{h {(\ln 2)}^{2}}{2!} + \frac{h^{2} {(\ln 2)}^{3}}{3!} + \dots]

= 2^{x} \ln 2

Commented by TawaTawa last updated on 17/Feb/20

God bless you sir