Question Number 129026 by oustmuchiya@gmail.com last updated on 12/Jan/21

$${differentiate}\:{y}=\frac{\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} \sqrt{\mathrm{6}{x}+\mathrm{2}}}{{x}^{\mathrm{3}} +\mathrm{1}} \\ $$
Answered by MJS_new last updated on 12/Jan/21
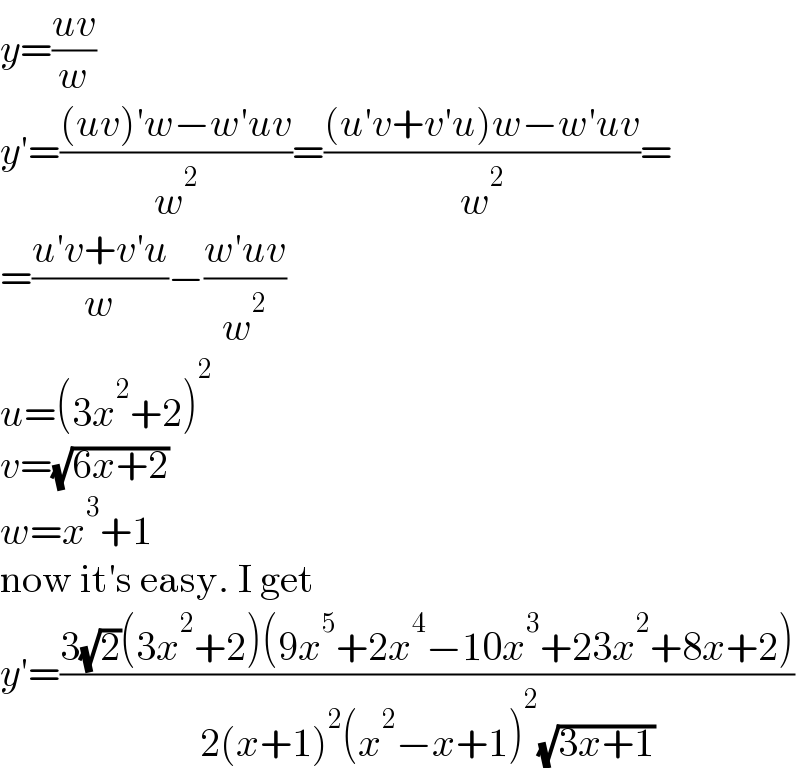
$${y}=\frac{{uv}}{{w}} \\ $$$${y}'=\frac{\left({uv}\right)'{w}−{w}'{uv}}{{w}^{\mathrm{2}} }=\frac{\left({u}'{v}+{v}'{u}\right){w}−{w}'{uv}}{{w}^{\mathrm{2}} }= \\ $$$$=\frac{{u}'{v}+{v}'{u}}{{w}}−\frac{{w}'{uv}}{{w}^{\mathrm{2}} } \\ $$$${u}=\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} \\ $$$${v}=\sqrt{\mathrm{6}{x}+\mathrm{2}} \\ $$$${w}={x}^{\mathrm{3}} +\mathrm{1} \\ $$$$\mathrm{now}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}.\:\mathrm{I}\:\mathrm{get} \\ $$$${y}'=\frac{\mathrm{3}\sqrt{\mathrm{2}}\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}\right)\left(\mathrm{9}{x}^{\mathrm{5}} +\mathrm{2}{x}^{\mathrm{4}} −\mathrm{10}{x}^{\mathrm{3}} +\mathrm{23}{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{2}\right)}{\mathrm{2}\left({x}+\mathrm{1}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} \sqrt{\mathrm{3}{x}+\mathrm{1}}} \\ $$
