Question Number 161311 by CM last updated on 15/Dec/21
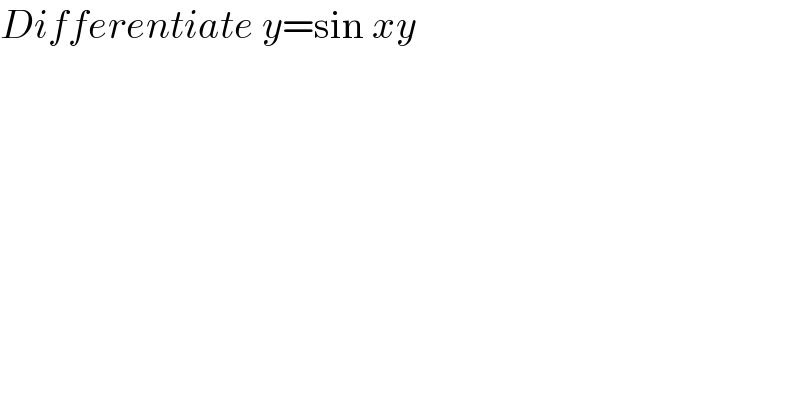
$${Differentiate}\:{y}=\mathrm{sin}\:{xy} \\ $$
Answered by mr W last updated on 15/Dec/21
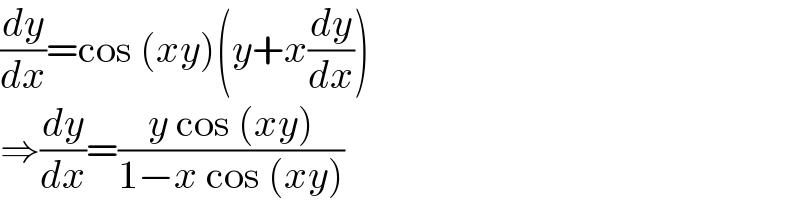
$$\frac{{dy}}{{dx}}=\mathrm{cos}\:\left({xy}\right)\left({y}+{x}\frac{{dy}}{{dx}}\right) \\ $$$$\Rightarrow\frac{{dy}}{{dx}}=\frac{{y}\:\mathrm{cos}\:\left({xy}\right)}{\mathrm{1}−{x}\:\mathrm{cos}\:\left({xy}\right)} \\ $$
Commented by CM last updated on 16/Dec/21

$${Thank}\:{you}\:{sir} \\ $$
Answered by 1549442205PVT last updated on 16/Dec/21
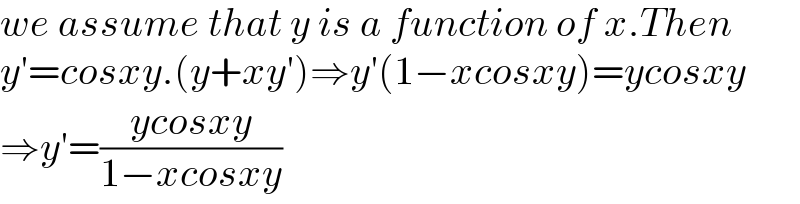
$${we}\:{assume}\:{that}\:{y}\:{is}\:{a}\:{function}\:{of}\:{x}.{Then} \\ $$$${y}'={cosxy}.\left({y}+{xy}'\right)\Rightarrow{y}'\left(\mathrm{1}−{xcosxy}\right)={ycosxy} \\ $$$$\Rightarrow{y}'=\frac{{ycosxy}}{\mathrm{1}−{xcosxy}} \\ $$
