Menu Close

Differentiate-y-x-x-1-hi-

Tinku Tara 0 Comments
Pin




Question Number 184188 by Mastermind last updated on 03/Jan/23
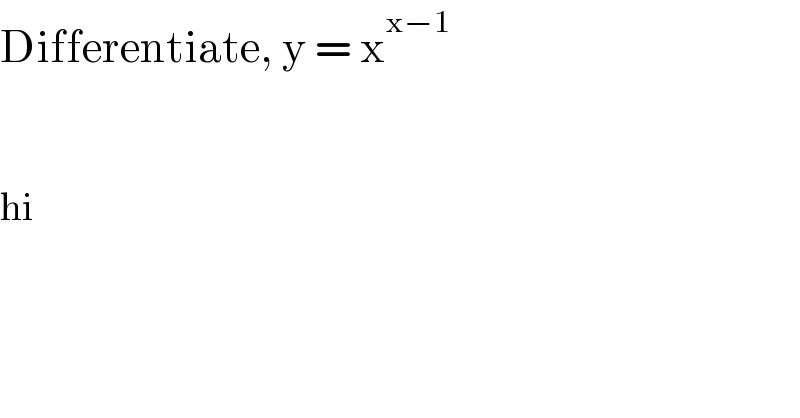
Differentiate, y = x^(x−1) hi
$$\mathrm{Differentiate},\:\mathrm{y}\:=\:\mathrm{x}^{\mathrm{x}−\mathrm{1}} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{hi} \\ $$
Answered by SEKRET last updated on 03/Jan/23
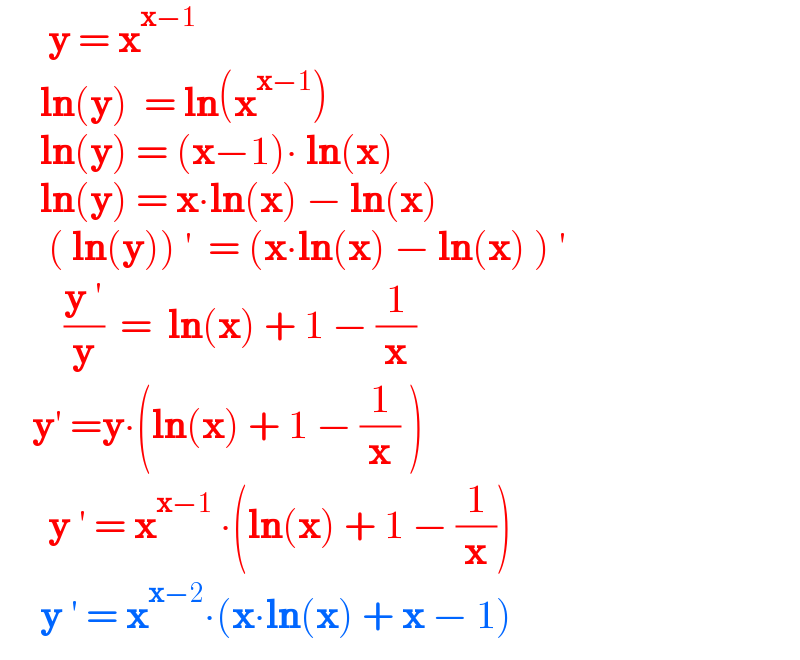
y = x^(x−1) ln(y) = ln(x^(x−1) ) ln(y) = (x−1)∙ ln(x) ln(y) = x∙ln(x) − ln(x) ( ln(y)) ′ = (x∙ln(x) − ln(x) ) ′ ((y ′)/y) = ln(x) + 1 − (1/x) y′ =y∙(ln(x) + 1 − (1/x) ) y ′ = x^(x−1) ∙(ln(x) + 1 − (1/x)) y ′ = x^(x−2) ∙(x∙ln(x) + x − 1)
$$\:\:\:\:\:\:\boldsymbol{\mathrm{y}}\:=\:\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}−\mathrm{1}} \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{y}}\right)\:\:=\:\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}−\mathrm{1}} \right) \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{y}}\right)\:=\:\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)\centerdot\:\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right) \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{y}}\right)\:=\:\boldsymbol{\mathrm{x}}\centerdot\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)\:−\:\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right) \\ $$$$\:\:\:\:\:\:\left(\:\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{y}}\right)\right)\:'\:\:=\:\left(\boldsymbol{\mathrm{x}}\centerdot\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)\:−\:\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)\:\right)\:' \\ $$$$\:\:\:\:\:\:\:\:\frac{\boldsymbol{\mathrm{y}}\:'}{\boldsymbol{\mathrm{y}}}\:\:=\:\:\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)\:+\:\mathrm{1}\:−\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{y}}'\:=\boldsymbol{\mathrm{y}}\centerdot\left(\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)\:+\:\mathrm{1}\:−\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}\:\right)\: \\ $$$$\:\:\:\:\:\:\boldsymbol{\mathrm{y}}\:'\:=\:\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}−\mathrm{1}} \:\centerdot\left(\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)\:+\:\mathrm{1}\:−\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}\right) \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{y}}\:'\:=\:\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}−\mathrm{2}} \centerdot\left(\boldsymbol{\mathrm{x}}\centerdot\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)\:+\:\boldsymbol{\mathrm{x}}\:−\:\mathrm{1}\right) \\ $$
Commented by Mastermind last updated on 03/Jan/23
Good!
$$\mathrm{Good}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *