Question Number 117865 by aurpeyz last updated on 14/Oct/20

$${discuss}\:{the}\:{lim}_{{n}\rightarrow\infty} \left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} \\ $$
Answered by 1549442205PVT last updated on 14/Oct/20
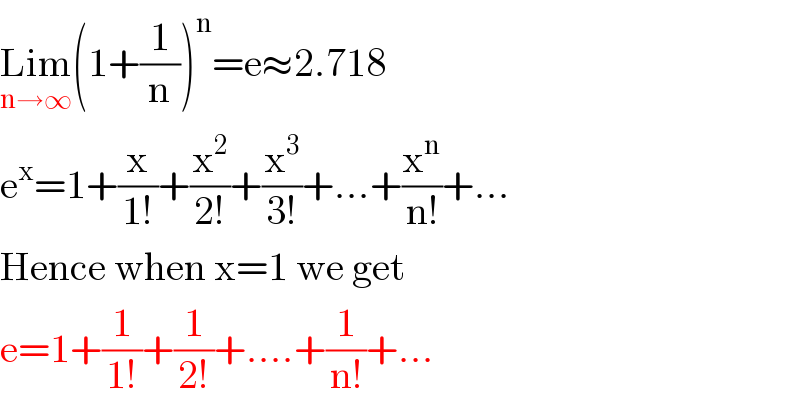
$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{Lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)^{\mathrm{n}} =\mathrm{e}\approx\mathrm{2}.\mathrm{718} \\ $$$$\mathrm{e}^{\mathrm{x}} =\mathrm{1}+\frac{\mathrm{x}}{\mathrm{1}!}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}!}+…+\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}!}+… \\ $$$$\mathrm{Hence}\:\mathrm{when}\:\mathrm{x}=\mathrm{1}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{e}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}+….+\frac{\mathrm{1}}{\mathrm{n}!}+… \\ $$
Answered by mhmoud last updated on 14/Oct/20

$$\mathrm{1} \\ $$
Answered by Lordose last updated on 14/Oct/20

$$\Lambda\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{n}}\right)^{\mathrm{n}} \\ $$$$\mathrm{ln}\Lambda=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{nln}\left\{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right\}\right) \\ $$$$\mathrm{set}\:\mathrm{u}=\frac{\mathrm{1}}{\mathrm{n}}\:\Rightarrow\:\left\{\mathrm{n}\rightarrow\infty,\:\mathrm{u}\rightarrow\mathrm{0}\right\} \\ $$$$\mathrm{ln}\Lambda\:=\:\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{u}\right)}{\mathrm{u}}\right) \\ $$$$\mathrm{L}\:\mathrm{hopital}'\mathrm{s} \\ $$$$\mathrm{ln}\Lambda\:=\:\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}}\right) \\ $$$$\mathrm{ln}\Lambda=\:\mathrm{1} \\ $$$$\Lambda\:=\:\mathrm{e}^{\mathrm{1}} \:=\:\mathrm{e} \\ $$
