Question Number 128574 by mohammad17 last updated on 08/Jan/21
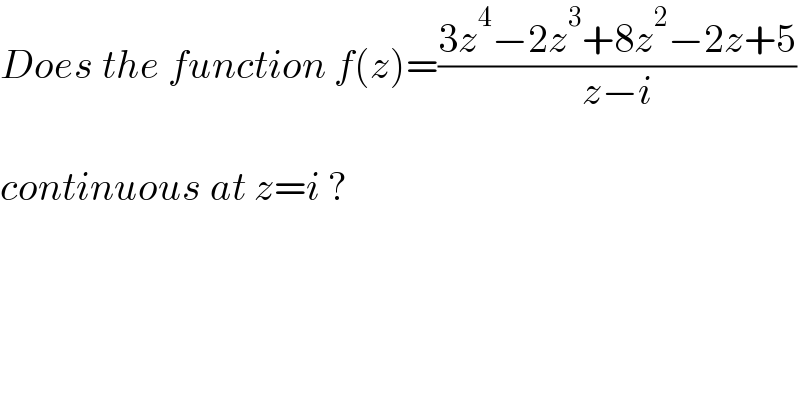
$${Does}\:{the}\:{function}\:{f}\left({z}\right)=\frac{\mathrm{3}{z}^{\mathrm{4}} −\mathrm{2}{z}^{\mathrm{3}} +\mathrm{8}{z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{5}}{{z}−{i}}\: \\ $$$$ \\ $$$${continuous}\:{at}\:{z}={i}\:? \\ $$
Answered by MJS_new last updated on 08/Jan/21
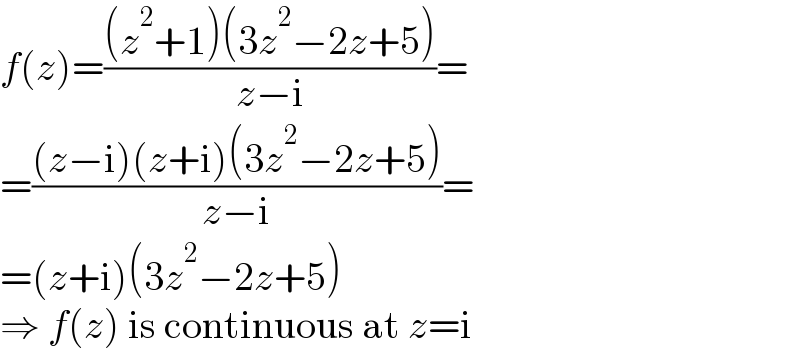
$${f}\left({z}\right)=\frac{\left({z}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{3}{z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{5}\right)}{{z}−\mathrm{i}}= \\ $$$$=\frac{\left({z}−\mathrm{i}\right)\left({z}+\mathrm{i}\right)\left(\mathrm{3}{z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{5}\right)}{{z}−\mathrm{i}}= \\ $$$$=\left({z}+\mathrm{i}\right)\left(\mathrm{3}{z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{5}\right) \\ $$$$\Rightarrow\:{f}\left({z}\right)\:\mathrm{is}\:\mathrm{continuous}\:\mathrm{at}\:{z}=\mathrm{i} \\ $$
