Menu Close

does-the-series-n-1-e-2-n-1-sin-npi-2-is-converge-or-diverge-

Tinku Tara 0 Comments
Pin




Question Number 169044 by mokys last updated on 23/Apr/22
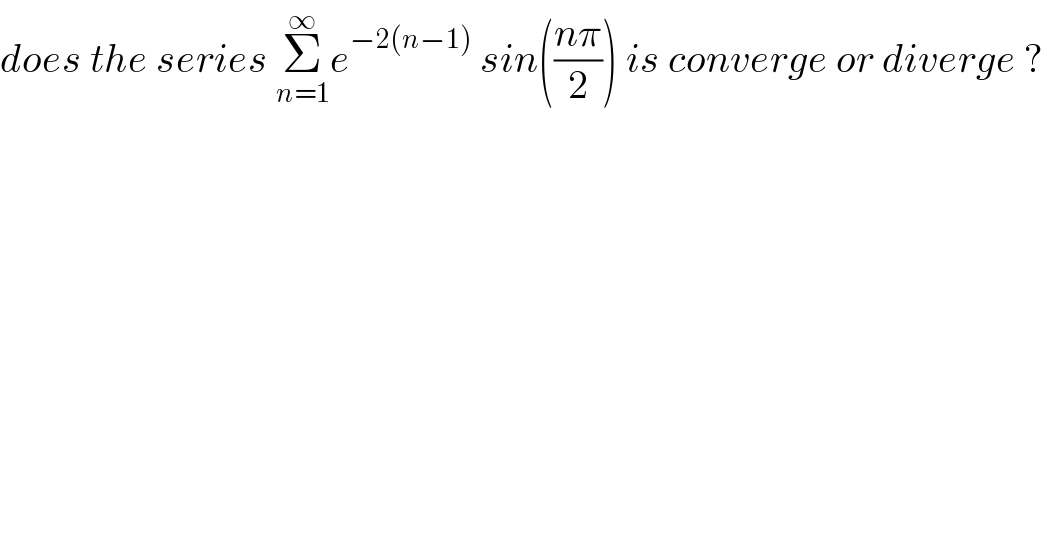
does the series Σ_(n=1) ^∞ e^(−2(n−1)) sin(((nπ)/2)) is converge or diverge ?
$${does}\:{the}\:{series}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{e}^{−\mathrm{2}\left({n}−\mathrm{1}\right)} \:{sin}\left(\frac{{n}\pi}{\mathrm{2}}\right)\:{is}\:{converge}\:{or}\:{diverge}\:? \\ $$
Answered by Mathspace last updated on 23/Apr/22
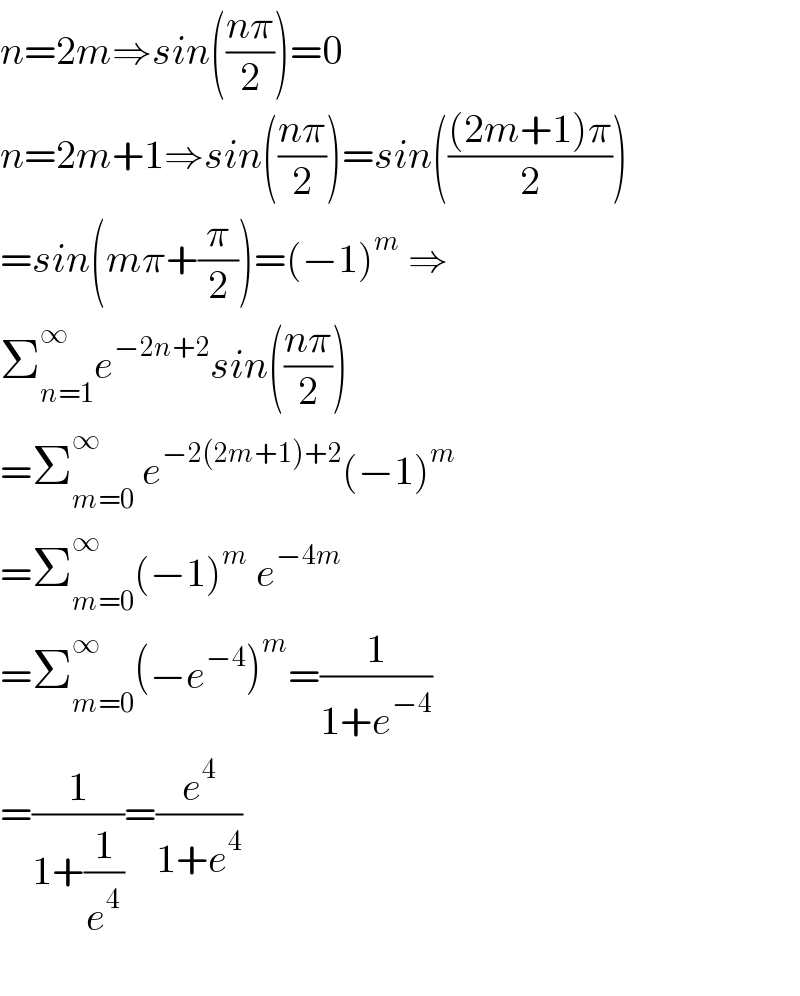
n=2m⇒sin(((nπ)/2))=0 n=2m+1⇒sin(((nπ)/2))=sin((((2m+1)π)/2)) =sin(mπ+(π/2))=(−1)^m ⇒ Σ_(n=1) ^(∞ ) e^(−2n+2) sin(((nπ)/2)) =Σ_(m=0) ^∞ e^(−2(2m+1)+2) (−1)^m =Σ_(m=0) ^∞ (−1)^m e^(−4m) =Σ_(m=0) ^∞ (−e^(−4) )^m =(1/(1+e^(−4) )) =(1/(1+(1/e^4 )))=(e^4 /(1+e^4 ))
$${n}=\mathrm{2}{m}\Rightarrow{sin}\left(\frac{{n}\pi}{\mathrm{2}}\right)=\mathrm{0} \\ $$$${n}=\mathrm{2}{m}+\mathrm{1}\Rightarrow{sin}\left(\frac{{n}\pi}{\mathrm{2}}\right)={sin}\left(\frac{\left(\mathrm{2}{m}+\mathrm{1}\right)\pi}{\mathrm{2}}\right) \\ $$$$={sin}\left({m}\pi+\frac{\pi}{\mathrm{2}}\right)=\left(−\mathrm{1}\right)^{{m}} \:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty\:} {e}^{−\mathrm{2}{n}+\mathrm{2}} {sin}\left(\frac{{n}\pi}{\mathrm{2}}\right) \\ $$$$=\sum_{{m}=\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{2}\left(\mathrm{2}{m}+\mathrm{1}\right)+\mathrm{2}} \left(−\mathrm{1}\right)^{{m}} \\ $$$$=\sum_{{m}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{m}} \:{e}^{−\mathrm{4}{m}} \\ $$$$=\sum_{{m}=\mathrm{0}} ^{\infty} \left(−{e}^{−\mathrm{4}} \right)^{{m}} =\frac{\mathrm{1}}{\mathrm{1}+{e}^{−\mathrm{4}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{{e}^{\mathrm{4}} }}=\frac{{e}^{\mathrm{4}} }{\mathrm{1}+{e}^{\mathrm{4}} } \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *