does-this-matter-reasonable-sin-x-x-dx-

Question Number 79580 by john santu last updated on 26/Jan/20

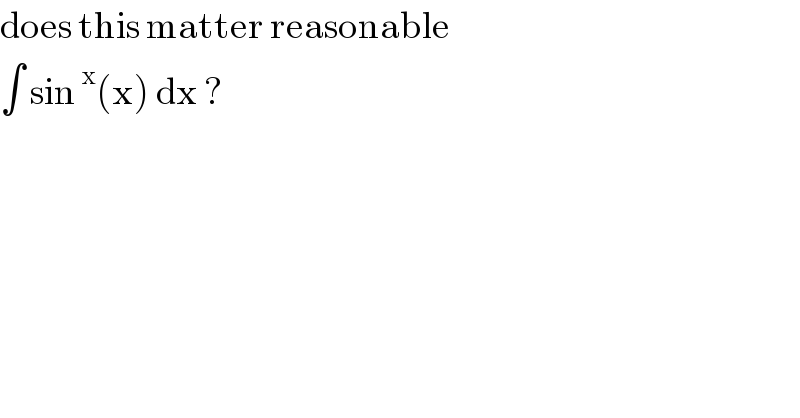
$$\mathrm{does}\:\mathrm{this}\:\mathrm{matter}\:\mathrm{reasonable} \\ $$$$\int\:\mathrm{sin}\:^{\mathrm{x}} \left(\mathrm{x}\right)\:\mathrm{dx}\:? \\ $$

Commented by MJS last updated on 26/Jan/20

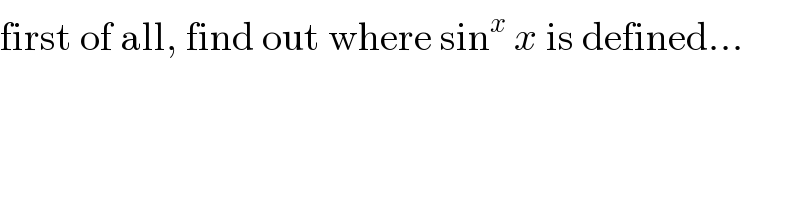
first of all, find out where sin^x x is defined...

$$\mathrm{first}\:\mathrm{of}\:\mathrm{all},\:\mathrm{find}\:\mathrm{out}\:\mathrm{where}\:\mathrm{sin}^{{x}} \:{x}\:\mathrm{is}\:\mathrm{defined}… \\ $$

Commented by john santu last updated on 26/Jan/20

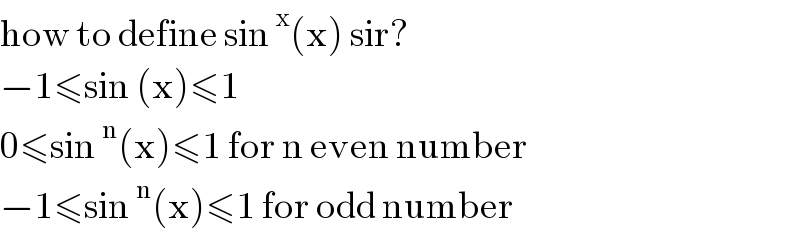
how to define sin^x (x) sir? −1≤sin (x)≤1 0≤sin^n (x)≤1 for n even number −1≤sin^n (x)≤1 for odd number

$$\mathrm{how}\:\mathrm{to}\:\mathrm{define}\:\mathrm{sin}\:^{\mathrm{x}} \left(\mathrm{x}\right)\:\mathrm{sir}? \\ $$$$−\mathrm{1}\leqslant\mathrm{sin}\:\left(\mathrm{x}\right)\leqslant\mathrm{1} \\ $$$$\mathrm{0}\leqslant\mathrm{sin}\:^{\mathrm{n}} \left(\mathrm{x}\right)\leqslant\mathrm{1}\:\mathrm{for}\:\mathrm{n}\:\mathrm{even}\:\mathrm{number} \\ $$$$−\mathrm{1}\leqslant\mathrm{sin}\:^{\mathrm{n}} \left(\mathrm{x}\right)\leqslant\mathrm{1}\:\mathrm{for}\:\mathrm{odd}\:\mathrm{number} \\ $$

Commented by mr W last updated on 26/Jan/20

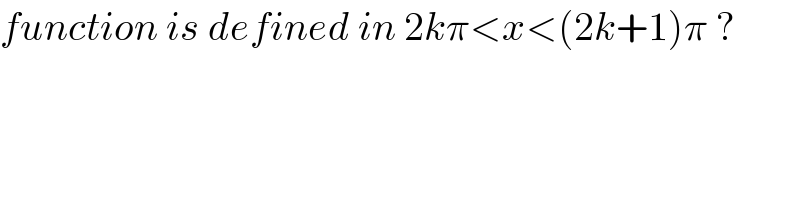
$${function}\:{is}\:{defined}\:{in}\:\mathrm{2}{k}\pi<{x}<\left(\mathrm{2}{k}+\mathrm{1}\right)\pi\:? \\ $$

Commented by MJS last updated on 26/Jan/20

but for the integral x∈R y=(sin x)^x let t=sin x ⇒ −1≤t≤1 ⇔ x= { ((2nπ+arcsin t)),(((2n+1)π−arcsin t)) :} y_n = { (t^(2nπ+arcsin t) ),(t^((2n+1)π−arcsin t) ) :} y_n is defined for 0≤t≤1 for t<0 it′s harder

$$\mathrm{but}\:\mathrm{for}\:\mathrm{the}\:\mathrm{integral}\:{x}\in\mathbb{R} \\ $$$${y}=\left(\mathrm{sin}\:{x}\right)^{{x}} \\ $$$$\mathrm{let}\:{t}=\mathrm{sin}\:{x}\:\Rightarrow\:−\mathrm{1}\leqslant{t}\leqslant\mathrm{1} \\ $$$$\Leftrightarrow\:{x}=\begin{cases}{\mathrm{2}{n}\pi+\mathrm{arcsin}\:{t}}\\{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi−\mathrm{arcsin}\:{t}}\end{cases} \\ $$$${y}_{{n}} =\begin{cases}{{t}^{\mathrm{2}{n}\pi+\mathrm{arcsin}\:{t}} }\\{{t}^{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi−\mathrm{arcsin}\:{t}} }\end{cases} \\ $$$${y}_{{n}} \:\mathrm{is}\:\mathrm{defined}\:\mathrm{for}\:\mathrm{0}\leqslant{t}\leqslant\mathrm{1} \\ $$$$\mathrm{for}\:{t}<\mathrm{0}\:\mathrm{it}'\mathrm{s}\:\mathrm{harder} \\ $$

Commented by john santu last updated on 26/Jan/20

there is no explanation , at which he is defined

$$\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{explanation}\:,\:\mathrm{at}\:\mathrm{which} \\ $$$$\mathrm{he}\:\mathrm{is}\:\mathrm{defined} \\ $$

Facebook Tweet Pin

does-this-matter-reasonable-sin-x-x-dx-

Leave a Reply Cancel reply