Menu Close

dt-3sint-4cost-

Tinku Tara 0 Comments
Pin




Question Number 92910 by s.ayeni14@yahoo.com last updated on 09/May/20
∫(dt/(3sint+4cost))
$$\int\frac{\mathrm{dt}}{\mathrm{3sint}+\mathrm{4cost}} \\ $$
Commented by msup by abdo last updated on 09/May/20
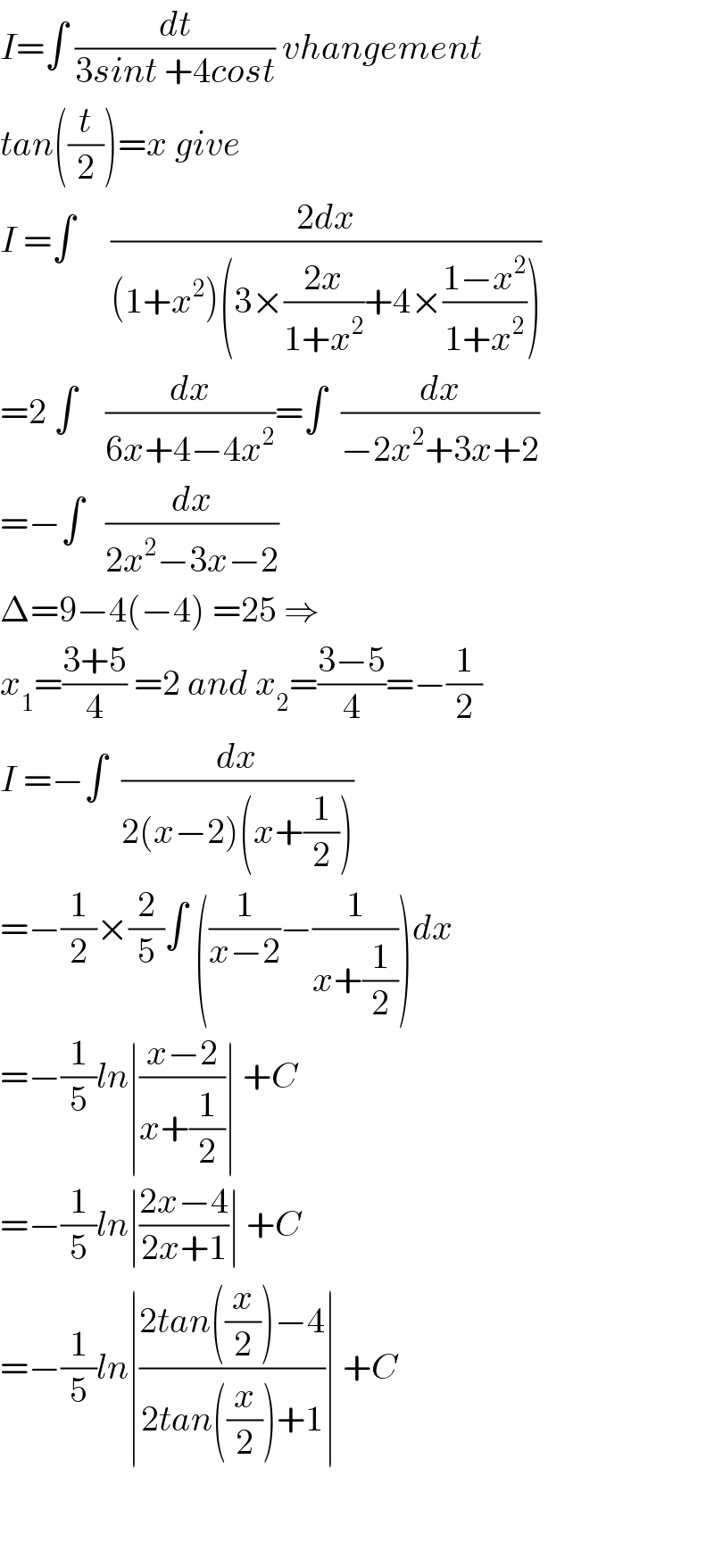
I=∫ (dt/(3sint +4cost)) vhangement tan((t/2))=x give I =∫ ((2dx)/((1+x^2 )(3×((2x)/(1+x^2 ))+4×((1−x^2 )/(1+x^2 ))))) =2 ∫ (dx/(6x+4−4x^2 ))=∫ (dx/(−2x^2 +3x+2)) =−∫ (dx/(2x^2 −3x−2)) Δ=9−4(−4) =25 ⇒ x_1 =((3+5)/4) =2 and x_2 =((3−5)/4)=−(1/2) I =−∫ (dx/(2(x−2)(x+(1/2)))) =−(1/2)×(2/5)∫ ((1/(x−2))−(1/(x+(1/2))))dx =−(1/5)ln∣((x−2)/(x+(1/2)))∣ +C =−(1/5)ln∣((2x−4)/(2x+1))∣ +C =−(1/5)ln∣((2tan((x/2))−4)/(2tan((x/2))+1))∣ +C
$${I}=\int\:\frac{{dt}}{\mathrm{3}{sint}\:+\mathrm{4}{cost}}\:{vhangement} \\ $$$${tan}\left(\frac{{t}}{\mathrm{2}}\right)={x}\:{give} \\ $$$${I}\:=\int\:\:\:\:\:\frac{\mathrm{2}{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{3}×\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }+\mathrm{4}×\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\right)} \\ $$$$=\mathrm{2}\:\int\:\:\:\:\frac{{dx}}{\mathrm{6}{x}+\mathrm{4}−\mathrm{4}{x}^{\mathrm{2}} }=\int\:\:\frac{{dx}}{−\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{2}} \\ $$$$=−\int\:\:\:\frac{{dx}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{2}} \\ $$$$\Delta=\mathrm{9}−\mathrm{4}\left(−\mathrm{4}\right)\:=\mathrm{25}\:\Rightarrow \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{3}+\mathrm{5}}{\mathrm{4}}\:=\mathrm{2}\:{and}\:{x}_{\mathrm{2}} =\frac{\mathrm{3}−\mathrm{5}}{\mathrm{4}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${I}\:=−\int\:\:\frac{{dx}}{\mathrm{2}\left({x}−\mathrm{2}\right)\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{5}}\int\:\left(\frac{\mathrm{1}}{{x}−\mathrm{2}}−\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{\mathrm{2}}}\right){dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{5}}{ln}\mid\frac{{x}−\mathrm{2}}{{x}+\frac{\mathrm{1}}{\mathrm{2}}}\mid\:+{C} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{5}}{ln}\mid\frac{\mathrm{2}{x}−\mathrm{4}}{\mathrm{2}{x}+\mathrm{1}}\mid\:+{C} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{5}}{ln}\mid\frac{\mathrm{2}{tan}\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{4}}{\mathrm{2}{tan}\left(\frac{{x}}{\mathrm{2}}\right)+\mathrm{1}}\mid\:+{C} \\ $$$$ \\ $$$$ \\ $$
Commented by i jagooll last updated on 10/May/20
(1/5)∫ (dt/(cos (t−θ))) , where tan θ=(3/4) = (1/5)∫ sec (t−θ) d(t−θ) =(1/5)ln ∣sec (t−θ)+tan (t−θ)∣ +c = (1/5)ln ∣(1/(cos tcos θ+sin tsin θ))+((tan t−tan θ)/(1+tan t.tan θ))∣+c =(1/5)ln∣(1/((4/5)cos t+(3/5)sin t)) +((tan t−(3/4))/(1+(3/4)tan t))∣+c
$$\frac{\mathrm{1}}{\mathrm{5}}\int\:\frac{\mathrm{dt}}{\mathrm{cos}\:\left(\mathrm{t}−\theta\right)}\:,\:\mathrm{where}\:\mathrm{tan}\:\theta=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{5}}\int\:\mathrm{sec}\:\left(\mathrm{t}−\theta\right)\:\mathrm{d}\left(\mathrm{t}−\theta\right)\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln}\:\mid\mathrm{sec}\:\left(\mathrm{t}−\theta\right)+\mathrm{tan}\:\left(\mathrm{t}−\theta\right)\mid\:+\mathrm{c}\: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln}\:\mid\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{tcos}\:\theta+\mathrm{sin}\:\mathrm{tsin}\:\theta}+\frac{\mathrm{tan}\:\mathrm{t}−\mathrm{tan}\:\theta}{\mathrm{1}+\mathrm{tan}\:\mathrm{t}.\mathrm{tan}\:\theta}\mid+\mathrm{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln}\mid\frac{\mathrm{1}}{\frac{\mathrm{4}}{\mathrm{5}}\mathrm{cos}\:\mathrm{t}+\frac{\mathrm{3}}{\mathrm{5}}\mathrm{sin}\:\mathrm{t}}\:+\frac{\mathrm{tan}\:\mathrm{t}−\frac{\mathrm{3}}{\mathrm{4}}}{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{tan}\:\mathrm{t}}\mid+\mathrm{c} \\ $$
Answered by mr W last updated on 09/May/20
=(1/5)∫(dt/((3/5) sin t+(4/5) cos t)) =(1/5)∫(dt/(sin α sin t+cos α cos t)) =(1/5)∫((d(t−α))/(cos (t−α))) =(1/5)∫(du/(cos u)) with u=t−α =(1/5)∫((d (sin u))/(1−sin^2 u)) =(1/5)∫(dv/(1−v^2 )) with v=sin u=sin (t−α) =(1/(10))∫((1/(1−v))+(1/(1+v)))dv =(1/(10))ln ∣((1+v)/(1−v))∣+C =(1/(10))ln ∣((1+sin (t−α))/(1−sin (t−α)))∣+C =(1/(10))ln ∣((1+sin t cos α−sin α cos t)/(1−sin t cos α+sin α cos t))∣+C =(1/(10))ln ∣((5+4 sin t−3 cos t)/(5−4 sin t+3 cos t))∣+C
$$=\frac{\mathrm{1}}{\mathrm{5}}\int\frac{{dt}}{\frac{\mathrm{3}}{\mathrm{5}}\:\mathrm{sin}\:{t}+\frac{\mathrm{4}}{\mathrm{5}}\:\mathrm{cos}\:{t}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\int\frac{{dt}}{\mathrm{sin}\:\alpha\:\mathrm{sin}\:{t}+\mathrm{cos}\:\alpha\:\mathrm{cos}\:{t}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\int\frac{{d}\left({t}−\alpha\right)}{\mathrm{cos}\:\left({t}−\alpha\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\int\frac{{du}}{\mathrm{cos}\:{u}}\:{with}\:{u}={t}−\alpha \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\int\frac{{d}\:\left(\mathrm{sin}\:{u}\right)}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\:{u}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\int\frac{{dv}}{\mathrm{1}−{v}^{\mathrm{2}} }\:{with}\:{v}=\mathrm{sin}\:{u}=\mathrm{sin}\:\left({t}−\alpha\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}\int\left(\frac{\mathrm{1}}{\mathrm{1}−{v}}+\frac{\mathrm{1}}{\mathrm{1}+{v}}\right){dv} \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}\mathrm{ln}\:\mid\frac{\mathrm{1}+{v}}{\mathrm{1}−{v}}\mid+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}\mathrm{ln}\:\mid\frac{\mathrm{1}+\mathrm{sin}\:\left({t}−\alpha\right)}{\mathrm{1}−\mathrm{sin}\:\left({t}−\alpha\right)}\mid+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}\mathrm{ln}\:\mid\frac{\mathrm{1}+\mathrm{sin}\:{t}\:\mathrm{cos}\:\alpha−\mathrm{sin}\:\alpha\:\mathrm{cos}\:{t}}{\mathrm{1}−\mathrm{sin}\:{t}\:\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha\:\mathrm{cos}\:{t}}\mid+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}\mathrm{ln}\:\mid\frac{\mathrm{5}+\mathrm{4}\:\mathrm{sin}\:{t}−\mathrm{3}\:\mathrm{cos}\:{t}}{\mathrm{5}−\mathrm{4}\:\mathrm{sin}\:{t}+\mathrm{3}\:\mathrm{cos}\:{t}}\mid+{C} \\ $$
Commented by s.ayeni14@yahoo.com last updated on 09/May/20
sir how?
$$\mathrm{sir}\:\mathrm{how}? \\ $$
Commented by mr W last updated on 09/May/20
how are you?
$${how}\:{are}\:{you}? \\ $$
Commented by s.ayeni14@yahoo.com last updated on 09/May/20
by the integrals of the form ∫(1/(a+bsint+ccost))dt then set x=(t/2)
$$\mathrm{by}\:\mathrm{the}\:\mathrm{integrals}\:\mathrm{of}\:\mathrm{the}\:\mathrm{form}\:\int\frac{\mathrm{1}}{\mathrm{a}+\mathrm{bsint}+\mathrm{ccost}}\mathrm{dt} \\ $$$$\mathrm{then}\:\mathrm{set}\:\mathrm{x}=\frac{\mathrm{t}}{\mathrm{2}} \\ $$
Commented by mr W last updated on 09/May/20
what happens if one doesn′t do that way but solves the question nevertheless?
$${what}\:{happens}\:{if}\:{one}\:{doesn}'{t}\:{do}\:{that} \\ $$$${way}\:{but}\:{solves}\:{the}\:{question}\:{nevertheless}? \\ $$
Commented by mr W last updated on 09/May/20
can you tell me where the error is in my way?
$${can}\:{you}\:{tell}\:{me}\:{where}\:{the}\:{error}\:{is}\:{in}\:{my} \\ $$$${way}? \\ $$
Commented by Ar Brandon last updated on 09/May/20
��It wasn't gonna make a great difference if Mr W used the same method everyone's currently using to arrive at the answer. Thanks Mr W for drawing my attention to your method.��
Commented by Ar Brandon last updated on 09/May/20
I understood your method and now feel I could arrive at the answer at level (1/5)∫(1/(cos u))du=(1/5)ln∣sec u+tan u∣
$$\mathrm{I}\:\mathrm{understood}\:\mathrm{your}\:\mathrm{method}\:\mathrm{and}\:\mathrm{now}\:\mathrm{feel} \\ $$$$\mathrm{I}\:\mathrm{could}\:\mathrm{arrive}\:\mathrm{at}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{at}\:\mathrm{level} \\ $$$$\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{u}}\mathrm{du}=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln}\mid\mathrm{sec}\:\mathrm{u}+\mathrm{tan}\:\mathrm{u}\mid \\ $$
Answered by s.ayeni14@yahoo.com last updated on 09/May/20
x=tan(t/2) 3sint+4cost=((6x)/(1+x^2 ))+((4(1−3^2 ))/(1+x^2 )) =((4+6x−4x^2 )/(1+x^2 )) ∫(dt/(3sint+4cost))=∫((1+x^2 )/(4+6x−4x^2 ))(((2dx)/(1+x^2 ))) =∫(1/(2+3x−2x^2 ))dx =(1/2)∫(1/(1+(3/2)−x^2 ))dx 1+(3/2)x−x^2 =((5/4))^2 −(x−(3/4))^2 (1/2)∫(1/(((5/4))^2 −(x−(3/4))^2 ))dx=(1/5)ln{((1+2x)/(4−2x))}+C =(1/5)ln{((1+2tan(t/2))/(4−2tan(t/2)))}+C
$$\mathrm{x}=\mathrm{tan}\frac{\mathrm{t}}{\mathrm{2}} \\ $$$$\mathrm{3sint}+\mathrm{4cost}=\frac{\mathrm{6x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{4}\left(\mathrm{1}−\mathrm{3}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{4}+\mathrm{6x}−\mathrm{4x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$\int\frac{\mathrm{dt}}{\mathrm{3sint}+\mathrm{4cost}}=\int\frac{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }{\mathrm{4}+\mathrm{6x}−\mathrm{4x}^{\mathrm{2}} }\left(\frac{\mathrm{2dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right) \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{2}+\mathrm{3x}−\mathrm{2x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}−\mathrm{x}^{\mathrm{2}} =\left(\frac{\mathrm{5}}{\mathrm{4}}\right)^{\mathrm{2}} −\left(\mathrm{x}−\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{\left(\frac{\mathrm{5}}{\mathrm{4}}\right)^{\mathrm{2}} −\left(\mathrm{x}−\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} }\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln}\left\{\frac{\mathrm{1}+\mathrm{2x}}{\mathrm{4}−\mathrm{2x}}\right\}+\mathrm{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln}\left\{\frac{\mathrm{1}+\mathrm{2tan}\frac{\mathrm{t}}{\mathrm{2}}}{\mathrm{4}−\mathrm{2tan}\frac{\mathrm{t}}{\mathrm{2}}}\right\}+\mathrm{C}\:\:\:\:\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *