Dterminer-la-valeur-de-x-

Facebook Tweet Pin

Question Number 181404 by a.lgnaoui last updated on 24/Nov/22

$${Dterminer}\:{la}\:{valeur}\:{de}\:\:\boldsymbol{{x}} \\ $$

Commented by mr W last updated on 24/Nov/22

$${generally}\:{there}\:{are}\:{two}\:{possible} \\ $$$${solutions}. \\ $$

Commented by mr W last updated on 24/Nov/22

Commented by a.lgnaoui last updated on 24/Nov/22

les segments AP BP PC sont determine par des mesures (non pas des medianes ni bissectrices) cela apparait claire dans (fig)

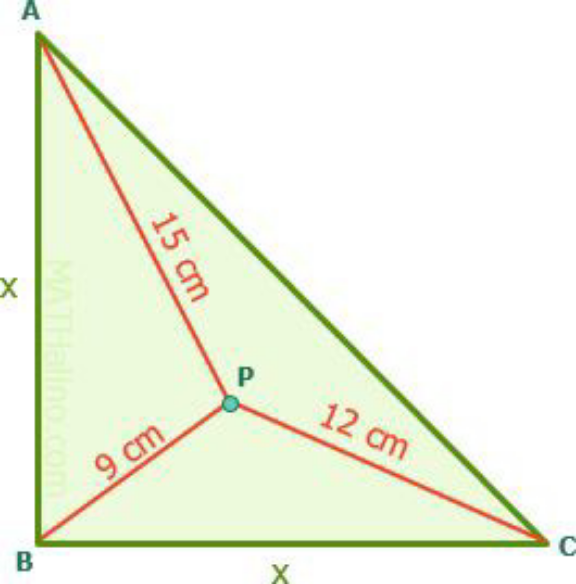
$${les}\:{segments}\:{AP}\:\:{BP}\:{PC}\:{sont}\:{determine} \\ $$$${par}\:{des}\:{mesures}\:\left({non}\:{pas}\:{des}\right. \\ $$$$\left.{medianes}\:\:{ni}\:{bissectrices}\right) \\ $$$${cela}\:{apparait}\:{claire}\:{dans}\:\left({fig}\right) \\ $$

Commented by a.lgnaoui last updated on 24/Nov/22

Commented by Acem last updated on 24/Nov/22

$${Salut}\:{monsioeur},\:{Me}'{dianes}\:{ou}\:{bissectrices} \\ $$$$\:{d}'{angles}? \\ $$

Answered by mr W last updated on 24/Nov/22

Commented by mr W last updated on 24/Nov/22

cos α=((x^2 +c^2 −a^2 )/(2cx)) cos β=((x^2 +c^2 −b^2 )/(2cx))=sin α (x^2 +c^2 −a^2 )^2 +(x^2 +c^2 −b^2 )^2 =4c^2 x^2 x^4 −(a^2 +b^2 )x^2 +((a^4 +b^4 )/2)−(a^2 +b^2 −c^2 )c^2 =0 x^2 =(1/2)[a^2 +b^2 ±(√(4(a^2 +b^2 −c^2 )c^2 −(a^2 −b^2 )^2 ))] ⇒x=(√((a^2 +b^2 ±(√(4(a^2 +b^2 −c^2 )c^2 −(a^2 −b^2 )^2 )))/2)) with a=15, b=12, c=9: x=(√((15^2 +12^2 ±(√(4(15^2 +12^2 −9^2 )9^2 −(15^2 −12^2 )^2 )))/2)) =((3(√(82±6(√(119)))))/2)≈18.214 or 6.102

$$\mathrm{cos}\:\alpha=\frac{{x}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{cx}} \\ $$$$\mathrm{cos}\:\beta=\frac{{x}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{cx}}=\mathrm{sin}\:\alpha \\ $$$$\left({x}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} +\left({x}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{4}{c}^{\mathrm{2}} {x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{4}} −\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){x}^{\mathrm{2}} +\frac{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} }{\mathrm{2}}−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right){c}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left[{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \pm\sqrt{\mathrm{4}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right){c}^{\mathrm{2}} −\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} }\right] \\ $$$$\Rightarrow{x}=\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \pm\sqrt{\mathrm{4}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right){c}^{\mathrm{2}} −\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} }}{\mathrm{2}}} \\ $$$${with}\:{a}=\mathrm{15},\:{b}=\mathrm{12},\:{c}=\mathrm{9}: \\ $$$${x}=\sqrt{\frac{\mathrm{15}^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} \pm\sqrt{\mathrm{4}\left(\mathrm{15}^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} −\mathrm{9}^{\mathrm{2}} \right)\mathrm{9}^{\mathrm{2}} −\left(\mathrm{15}^{\mathrm{2}} −\mathrm{12}^{\mathrm{2}} \right)^{\mathrm{2}} }}{\mathrm{2}}} \\ $$$$\:\:\:=\frac{\mathrm{3}\sqrt{\mathrm{82}\pm\mathrm{6}\sqrt{\mathrm{119}}}}{\mathrm{2}}\approx\mathrm{18}.\mathrm{214}\:{or}\:\mathrm{6}.\mathrm{102} \\ $$

Commented by a.lgnaoui last updated on 24/Nov/22