Menu Close

dx-1-cos-cos-x-

Tinku Tara 0 Comments
Pin




Question Number 120254 by bramlexs22 last updated on 30/Oct/20
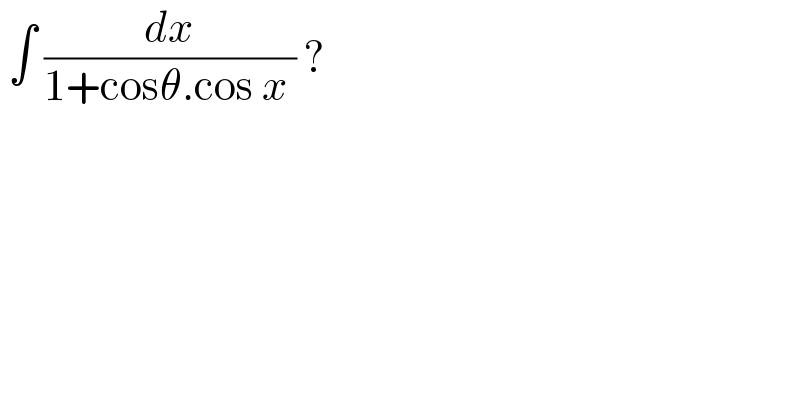
∫ (dx/(1+cosθ.cos x )) ?
$$\:\int\:\frac{{dx}}{\mathrm{1}+\mathrm{cos}\theta.\mathrm{cos}\:{x}\:}\:? \\ $$
Answered by TANMAY PANACEA last updated on 30/Oct/20
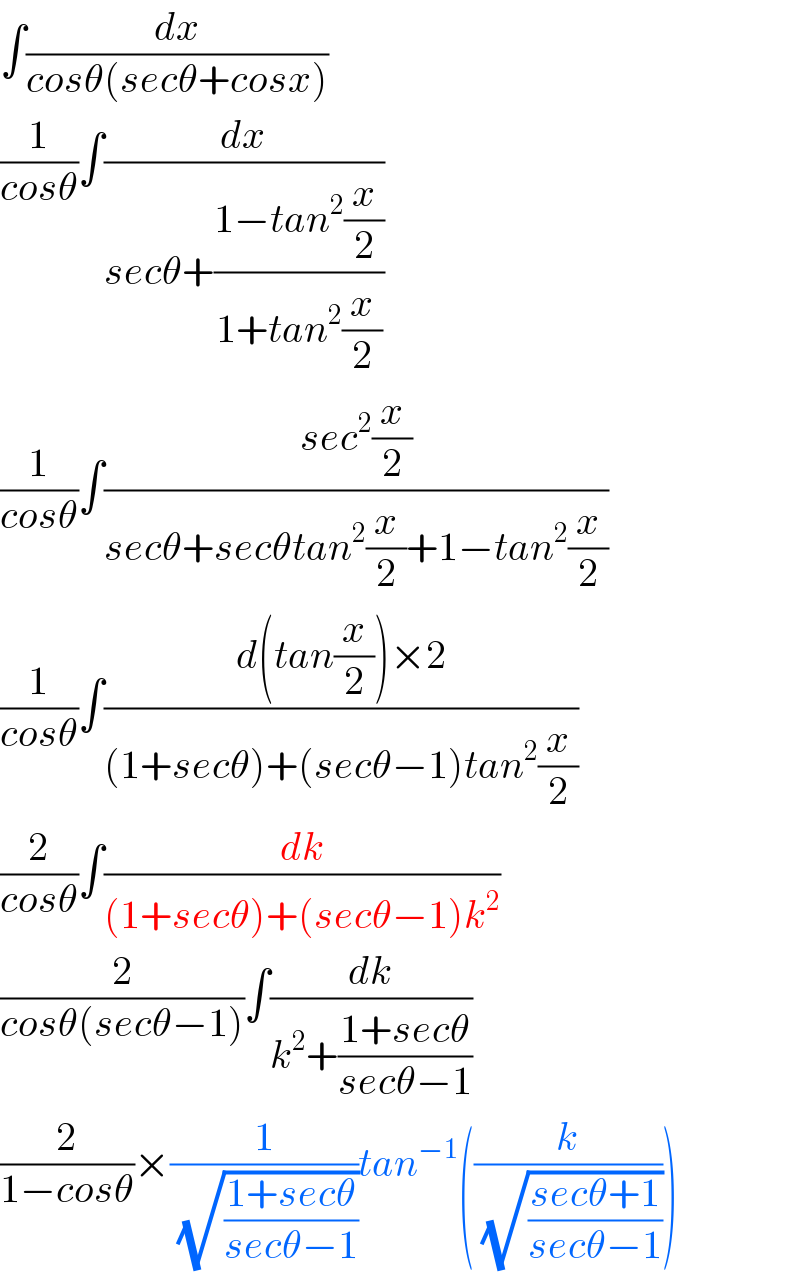
∫(dx/(cosθ(secθ+cosx))) (1/(cosθ))∫(dx/(secθ+((1−tan^2 (x/2))/(1+tan^2 (x/2))))) (1/(cosθ))∫((sec^2 (x/2))/(secθ+secθtan^2 (x/2)+1−tan^2 (x/2))) (1/(cosθ))∫((d(tan(x/2))×2)/((1+secθ)+(secθ−1)tan^2 (x/2))) (2/(cosθ))∫(dk/((1+secθ)+(secθ−1)k^2 )) (2/(cosθ(secθ−1)))∫(dk/(k^2 +((1+secθ)/(secθ−1)))) (2/(1−cosθ))×(1/( (√((1+secθ)/(secθ−1)))))tan^(−1) ((k/( (√((secθ+1)/(secθ−1))))))
$$\int\frac{{dx}}{{cos}\theta\left({sec}\theta+{cosx}\right)} \\ $$$$\frac{\mathrm{1}}{{cos}\theta}\int\frac{{dx}}{{sec}\theta+\frac{\mathrm{1}−{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{1}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}} \\ $$$$\frac{\mathrm{1}}{{cos}\theta}\int\frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{{sec}\theta+{sec}\theta{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+\mathrm{1}−{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}} \\ $$$$\frac{\mathrm{1}}{{cos}\theta}\int\frac{{d}\left({tan}\frac{{x}}{\mathrm{2}}\right)×\mathrm{2}}{\left(\mathrm{1}+{sec}\theta\right)+\left({sec}\theta−\mathrm{1}\right){tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}} \\ $$$$\frac{\mathrm{2}}{{cos}\theta}\int\frac{{dk}}{\left(\mathrm{1}+{sec}\theta\right)+\left({sec}\theta−\mathrm{1}\right){k}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{2}}{{cos}\theta\left({sec}\theta−\mathrm{1}\right)}\int\frac{{dk}}{{k}^{\mathrm{2}} +\frac{\mathrm{1}+{sec}\theta}{{sec}\theta−\mathrm{1}}} \\ $$$$\frac{\mathrm{2}}{\mathrm{1}−{cos}\theta}×\frac{\mathrm{1}}{\:\sqrt{\frac{\mathrm{1}+{sec}\theta}{{sec}\theta−\mathrm{1}}}}{tan}^{−\mathrm{1}} \left(\frac{{k}}{\:\sqrt{\frac{{sec}\theta+\mathrm{1}}{{sec}\theta−\mathrm{1}}}}\right) \\ $$
Answered by bemath last updated on 30/Oct/20
let cos θ = k ⇒ ∫ (dx/(1+kcos x)) let tan ((x/2)) = u ⇒ (1/2)sec^2 ((x/2))dx=du dx = 2cos^2 ((x/2)) du = ((2 du)/(1+u^2 )) I=∫ ((2 du)/((1+u^2 )(1+((k(1−u^2 ))/(1+u^2 ))))) I=∫ ((2 du)/((1+k)+(1−k)u^2 ))= ∫ ((2 du)/( ((√(1+k )))^2 +u^2 ((√(1−k)) )^2 )) letting u(√(1−k)) = (√(1+k)) tan w I= ∫ ((2 ((√((1+k)/(1−k))) ) sec^2 (w) dw)/((1+k)sec^2 (w))) I=(2/( (√(1−k^2 )))) w + c = (2/( (√(1−k^2 )))) arc tan (u (√((1−k)/(1+k))))+c = (2/( (√(1−cos^2 θ)))) arc tan (tan ((x/2))(√((1−cos θ)/(1+cos θ)))) + c = 2 cosec θ arc tan (tan ((x/2)) (√((1−cos θ)/(1+cos θ)))) + c
$${let}\:\mathrm{cos}\:\theta\:=\:{k}\:\Rightarrow\:\int\:\frac{{dx}}{\mathrm{1}+{k}\mathrm{cos}\:{x}} \\ $$$${let}\:\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)\:=\:{u}\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right){dx}={du} \\ $$$${dx}\:=\:\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\:{du}\:=\:\frac{\mathrm{2}\:{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$${I}=\int\:\frac{\mathrm{2}\:{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{{k}\left(\mathrm{1}−{u}^{\mathrm{2}} \right)}{\mathrm{1}+{u}^{\mathrm{2}} }\right)} \\ $$$${I}=\int\:\frac{\mathrm{2}\:{du}}{\left(\mathrm{1}+{k}\right)+\left(\mathrm{1}−{k}\right){u}^{\mathrm{2}} }=\:\int\:\frac{\mathrm{2}\:{du}}{\:\left(\sqrt{\mathrm{1}+{k}\:}\right)^{\mathrm{2}} \:+{u}^{\mathrm{2}} \:\left(\sqrt{\mathrm{1}−{k}}\:\right)^{\mathrm{2}} } \\ $$$${letting}\:{u}\sqrt{\mathrm{1}−{k}}\:=\:\sqrt{\mathrm{1}+{k}}\:\mathrm{tan}\:{w} \\ $$$${I}=\:\int\:\frac{\mathrm{2}\:\left(\sqrt{\frac{\mathrm{1}+{k}}{\mathrm{1}−{k}}}\:\right)\:\mathrm{sec}\:^{\mathrm{2}} \left({w}\right)\:{dw}}{\left(\mathrm{1}+{k}\right)\mathrm{sec}\:^{\mathrm{2}} \left({w}\right)} \\ $$$${I}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{k}^{\mathrm{2}} }}\:{w}\:+\:{c}\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{k}^{\mathrm{2}} }}\:\mathrm{arc}\:\mathrm{tan}\:\left({u}\:\sqrt{\frac{\mathrm{1}−{k}}{\mathrm{1}+{k}}}\right)+{c} \\ $$$$=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \theta}}\:\mathrm{arc}\:\mathrm{tan}\:\left(\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)\sqrt{\frac{\mathrm{1}−\mathrm{cos}\:\theta}{\mathrm{1}+\mathrm{cos}\:\theta}}\right)\:+\:{c} \\ $$$$=\:\mathrm{2}\:\mathrm{cosec}\:\theta\:\mathrm{arc}\:\mathrm{tan}\:\left(\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)\:\sqrt{\frac{\mathrm{1}−\mathrm{cos}\:\theta}{\mathrm{1}+\mathrm{cos}\:\theta}}\right)\:+\:{c} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 30/Oct/20
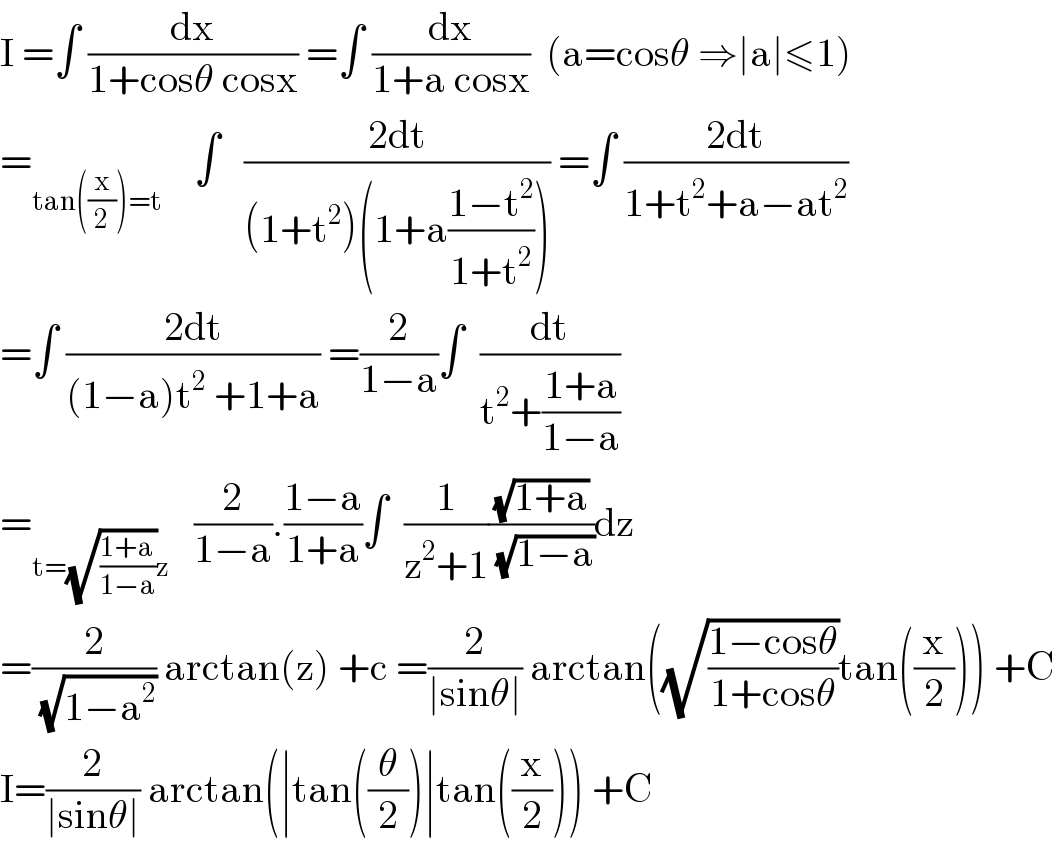
I =∫ (dx/(1+cosθ cosx)) =∫ (dx/(1+a cosx)) (a=cosθ ⇒∣a∣≤1) =_(tan((x/2))=t) ∫ ((2dt)/((1+t^2 )(1+a((1−t^2 )/(1+t^2 ))))) =∫ ((2dt)/(1+t^2 +a−at^2 )) =∫ ((2dt)/((1−a)t^2 +1+a)) =(2/(1−a))∫ (dt/(t^2 +((1+a)/(1−a)))) =_(t=(√((1+a)/(1−a)))z) (2/(1−a)).((1−a)/(1+a))∫ (1/(z^2 +1))((√(1+a))/( (√(1−a))))dz =(2/( (√(1−a^2 )))) arctan(z) +c =(2/(∣sinθ∣)) arctan((√((1−cosθ)/(1+cosθ)))tan((x/2))) +C I=(2/(∣sinθ∣)) arctan(∣tan((θ/2))∣tan((x/2))) +C
$$\mathrm{I}\:=\int\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{cos}\theta\:\mathrm{cosx}}\:=\int\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{a}\:\mathrm{cosx}}\:\:\left(\mathrm{a}=\mathrm{cos}\theta\:\Rightarrow\mid\mathrm{a}\mid\leqslant\mathrm{1}\right) \\ $$$$=_{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}} \:\:\:\:\int\:\:\:\frac{\mathrm{2dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{a}\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)}\:=\int\:\frac{\mathrm{2dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} +\mathrm{a}−\mathrm{at}^{\mathrm{2}} } \\ $$$$=\int\:\frac{\mathrm{2dt}}{\left(\mathrm{1}−\mathrm{a}\right)\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}+\mathrm{a}}\:=\frac{\mathrm{2}}{\mathrm{1}−\mathrm{a}}\int\:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{1}+\mathrm{a}}{\mathrm{1}−\mathrm{a}}} \\ $$$$=_{\mathrm{t}=\sqrt{\frac{\mathrm{1}+\mathrm{a}}{\mathrm{1}−\mathrm{a}}}\mathrm{z}} \:\:\:\frac{\mathrm{2}}{\mathrm{1}−\mathrm{a}}.\frac{\mathrm{1}−\mathrm{a}}{\mathrm{1}+\mathrm{a}}\int\:\:\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} +\mathrm{1}}\frac{\sqrt{\mathrm{1}+\mathrm{a}}}{\:\sqrt{\mathrm{1}−\mathrm{a}}}\mathrm{dz} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\:\mathrm{arctan}\left(\mathrm{z}\right)\:+\mathrm{c}\:=\frac{\mathrm{2}}{\mid\mathrm{sin}\theta\mid}\:\mathrm{arctan}\left(\sqrt{\frac{\mathrm{1}−\mathrm{cos}\theta}{\mathrm{1}+\mathrm{cos}\theta}}\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)\:+\mathrm{C} \\ $$$$\mathrm{I}=\frac{\mathrm{2}}{\mid\mathrm{sin}\theta\mid}\:\mathrm{arctan}\left(\mid\mathrm{tan}\left(\frac{\theta}{\mathrm{2}}\right)\mid\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)\:+\mathrm{C} \\ $$
Answered by Dwaipayan Shikari last updated on 30/Oct/20
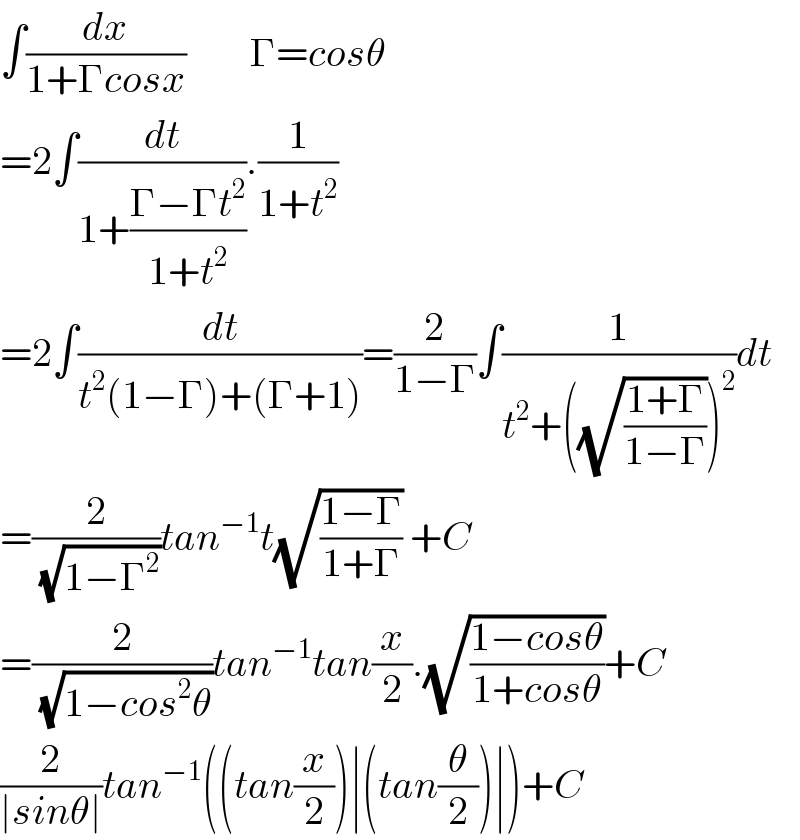
∫(dx/(1+Γcosx)) Γ=cosθ =2∫(dt/(1+((Γ−Γt^2 )/(1+t^2 )))).(1/(1+t^2 )) =2∫(dt/(t^2 (1−Γ)+(Γ+1)))=(2/(1−Γ))∫(1/(t^2 +((√((1+Γ)/(1−Γ))))^2 ))dt =(2/( (√(1−Γ^2 ))))tan^(−1) t(√((1−Γ)/(1+Γ))) +C =(2/( (√(1−cos^2 θ))))tan^(−1) tan(x/2).(√((1−cosθ)/(1+cosθ)))+C (2/(∣sinθ∣))tan^(−1) ((tan(x/2))∣(tan(θ/2))∣)+C
$$\int\frac{{dx}}{\mathrm{1}+\Gamma{cosx}}\:\:\:\:\:\:\:\:\Gamma={cos}\theta \\ $$$$=\mathrm{2}\int\frac{{dt}}{\mathrm{1}+\frac{\Gamma−\Gamma{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} \left(\mathrm{1}−\Gamma\right)+\left(\Gamma+\mathrm{1}\right)}=\frac{\mathrm{2}}{\mathrm{1}−\Gamma}\int\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\left(\sqrt{\frac{\mathrm{1}+\Gamma}{\mathrm{1}−\Gamma}}\right)^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\Gamma^{\mathrm{2}} }}{tan}^{−\mathrm{1}} {t}\sqrt{\frac{\mathrm{1}−\Gamma}{\mathrm{1}+\Gamma}}\:+{C} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{cos}^{\mathrm{2}} \theta}}{tan}^{−\mathrm{1}} {tan}\frac{{x}}{\mathrm{2}}.\sqrt{\frac{\mathrm{1}−{cos}\theta}{\mathrm{1}+{cos}\theta}}+{C} \\ $$$$\frac{\mathrm{2}}{\mid{sin}\theta\mid}{tan}^{−\mathrm{1}} \left(\left({tan}\frac{{x}}{\mathrm{2}}\right)\mid\left({tan}\frac{\theta}{\mathrm{2}}\right)\mid\right)+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *