Question Number 85667 by john santu last updated on 23/Mar/20
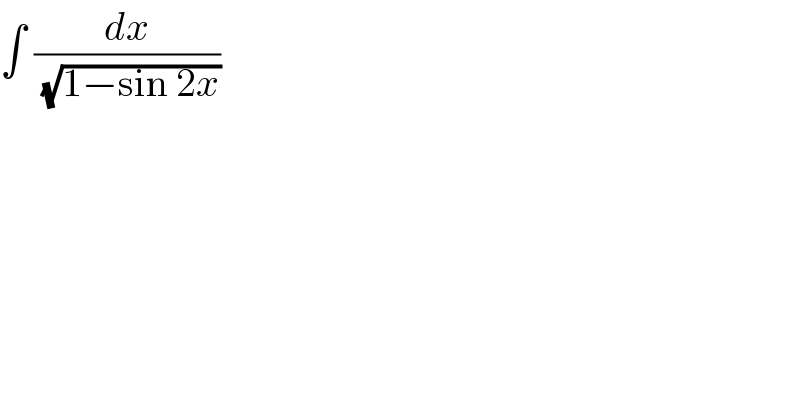
$$\int\:\frac{{dx}}{\:\sqrt{\mathrm{1}−\mathrm{sin}\:\mathrm{2}{x}}}\: \\ $$
Answered by som(math1967) last updated on 24/Mar/20

$$\int\frac{{dx}}{\left({cosx}−{sinx}\right)} \\ $$$$\int\frac{{dx}}{\:\sqrt{\mathrm{2}}{cos}\left({x}+\frac{\pi}{\mathrm{4}}\right)} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int{sec}\left({x}+\frac{\pi}{\mathrm{4}}\right){dx} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{ln}\mid{tan}\left(\frac{\pi}{\mathrm{4}}\:+\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{8}}\right)\mid+{C} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{ln}\mid{tan}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\:+\frac{{x}}{\mathrm{2}}\right)\mid\:+{C} \\ $$
Commented by jagoll last updated on 24/Mar/20

$$\mathrm{sir}\:\sqrt{\mathrm{1}−\mathrm{sin}\:\mathrm{2x}\:}=\:\mid\mathrm{cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}\mid \\ $$$$\mathrm{why}\:\sqrt{\mathrm{1}−\mathrm{sin}\:\mathrm{2x}}\:\:=\:\mathrm{cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}\:? \\ $$
Commented by jagoll last updated on 24/Mar/20

$$\mathrm{then}\:\int\:\mathrm{sec}\:\mathrm{x}\:\mathrm{dx}\:=\:\mathrm{ln}\:\mid\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}\mid\:\mathrm{sir} \\ $$
Commented by som(math1967) last updated on 24/Mar/20
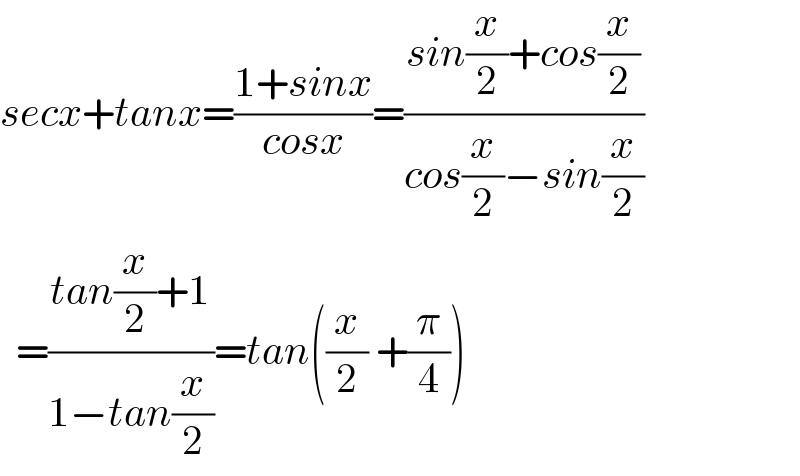
$${secx}+{tanx}=\frac{\mathrm{1}+{sinx}}{{cosx}}=\frac{{sin}\frac{{x}}{\mathrm{2}}+{cos}\frac{{x}}{\mathrm{2}}}{{cos}\frac{{x}}{\mathrm{2}}−{sin}\frac{{x}}{\mathrm{2}}} \\ $$$$\:\:=\frac{{tan}\frac{{x}}{\mathrm{2}}+\mathrm{1}}{\mathrm{1}−{tan}\frac{{x}}{\mathrm{2}}}={tan}\left(\frac{{x}}{\mathrm{2}}\:+\frac{\pi}{\mathrm{4}}\right) \\ $$
Commented by jagoll last updated on 24/Mar/20

$$\mathrm{oo}\:\mathrm{same}\:\mathrm{sir}.\:\mathrm{but}\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{agree} \\ $$$$\mathrm{with}\:\sqrt{\mathrm{1}−\mathrm{sin}\:\mathrm{2x}}\:=\:\mathrm{cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}\:\mathrm{sir} \\ $$
Commented by jagoll last updated on 24/Mar/20

$$\mathrm{i}\:\mathrm{got}\:\mathrm{two}\:\mathrm{solution}\: \\ $$
Commented by som(math1967) last updated on 24/Mar/20

$${yes}\:{two}\:{solution}\:{possible} \\ $$$${I}\:{use}\:{only}\:\left({cosx}−{sinx}\right) \\ $$
Commented by jagoll last updated on 24/Mar/20

$$\mathrm{yes}\:\mathrm{sir}.\:\mathrm{deal} \\ $$
Commented by john santu last updated on 24/Mar/20

$${yes}\:{have}\:\mathrm{2}\:{solution} \\ $$
