Question Number 97526 by student work last updated on 08/Jun/20

$$\int\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}=? \\ $$
Commented by bobhans last updated on 08/Jun/20
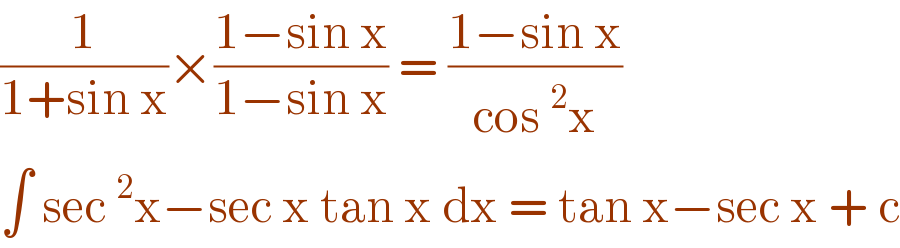
$$\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}×\frac{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}\:=\:\frac{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}} \\ $$$$\int\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}−\mathrm{sec}\:\mathrm{x}\:\mathrm{tan}\:\mathrm{x}\:\mathrm{dx}\:=\:\mathrm{tan}\:\mathrm{x}−\mathrm{sec}\:\mathrm{x}\:+\:\mathrm{c} \\ $$
Answered by smridha last updated on 08/Jun/20
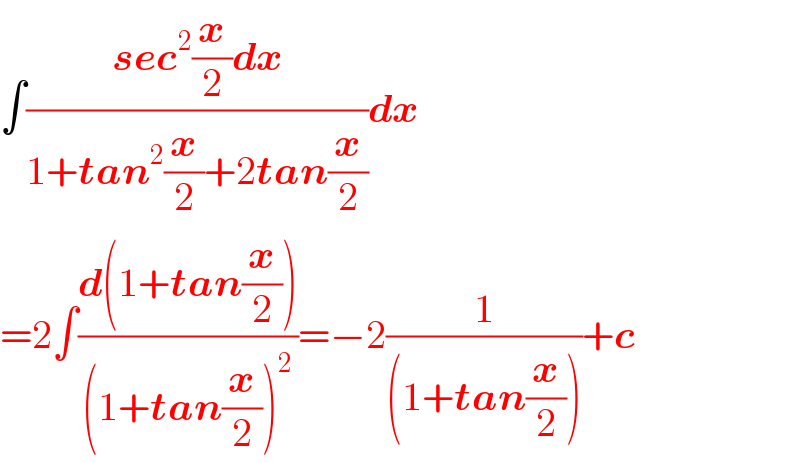
$$\int\frac{\boldsymbol{{sec}}^{\mathrm{2}} \frac{\boldsymbol{{x}}}{\mathrm{2}}\boldsymbol{{dx}}}{\mathrm{1}+\boldsymbol{{tan}}^{\mathrm{2}} \frac{\boldsymbol{{x}}}{\mathrm{2}}+\mathrm{2}\boldsymbol{{tan}}\frac{\boldsymbol{{x}}}{\mathrm{2}}}\boldsymbol{{dx}} \\ $$$$=\mathrm{2}\int\frac{\boldsymbol{{d}}\left(\mathrm{1}+\boldsymbol{{tan}}\frac{\boldsymbol{{x}}}{\mathrm{2}}\right)}{\left(\mathrm{1}+\boldsymbol{{tan}}\frac{\boldsymbol{{x}}}{\mathrm{2}}\right)^{\mathrm{2}} }=−\mathrm{2}\frac{\mathrm{1}}{\left(\mathrm{1}+\boldsymbol{{tan}}\frac{\boldsymbol{{x}}}{\mathrm{2}}\right)}+\boldsymbol{{c}} \\ $$
