Question Number 93869 by i jagooll last updated on 15/May/20

$$\int\:\frac{\mathrm{dx}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}\:? \\ $$
Commented by i jagooll last updated on 15/May/20
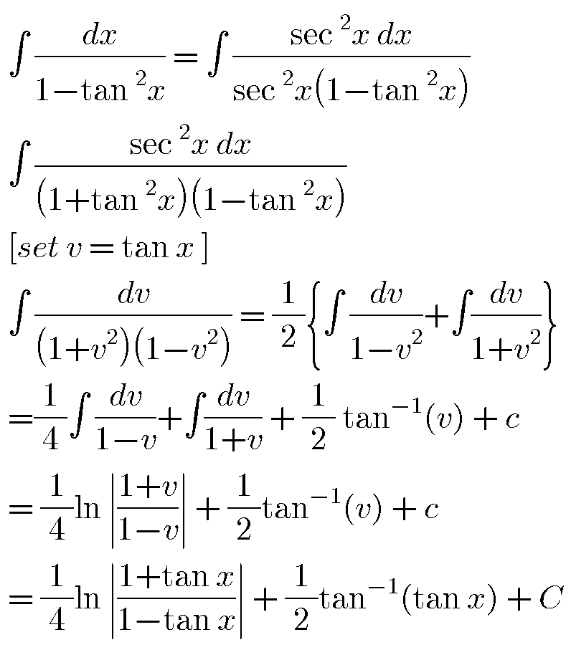
Commented by Tony Lin last updated on 15/May/20
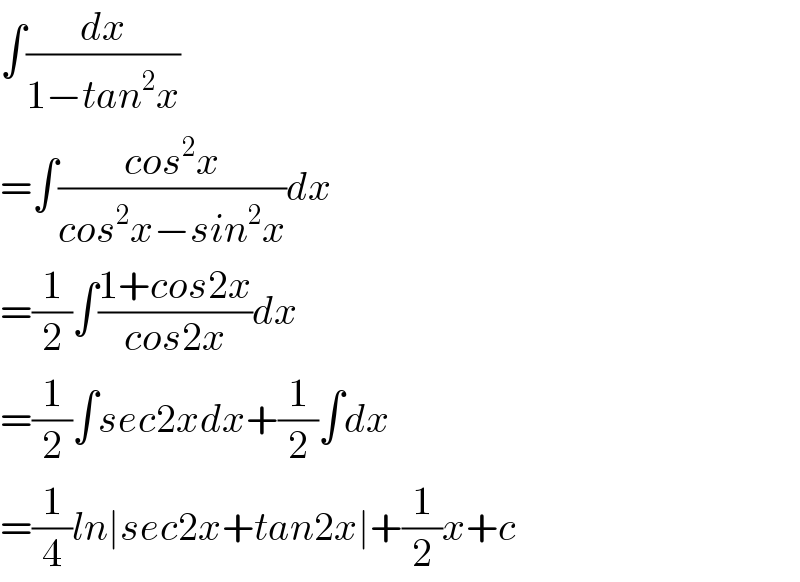
$$\int\frac{{dx}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}} \\ $$$$=\int\frac{{cos}^{\mathrm{2}} {x}}{{cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+{cos}\mathrm{2}{x}}{{cos}\mathrm{2}{x}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int{sec}\mathrm{2}{xdx}+\frac{\mathrm{1}}{\mathrm{2}}\int{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid{sec}\mathrm{2}{x}+{tan}\mathrm{2}{x}\mid+\frac{\mathrm{1}}{\mathrm{2}}{x}+{c} \\ $$
