Question Number 157977 by tounghoungko last updated on 30/Oct/21
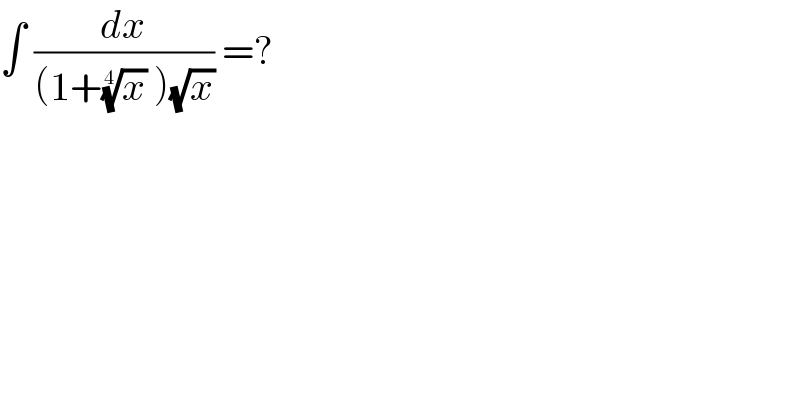
$$\int\:\frac{{dx}}{\left(\mathrm{1}+\sqrt[{\mathrm{4}}]{{x}}\:\right)\sqrt{{x}}}\:=? \\ $$
Answered by puissant last updated on 30/Oct/21
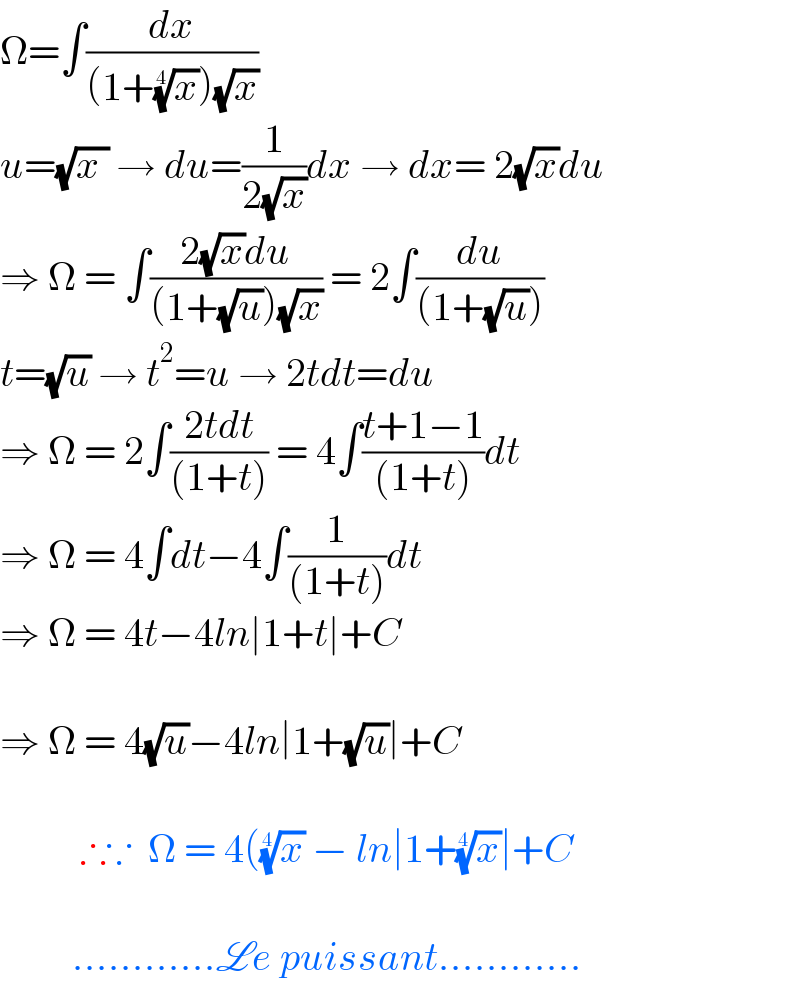
$$\Omega=\int\frac{{dx}}{\left(\mathrm{1}+\sqrt[{\mathrm{4}}]{{x}}\right)\sqrt{{x}}} \\ $$$${u}=\sqrt{{x}\:}\:\rightarrow\:{du}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}{dx}\:\rightarrow\:{dx}=\:\mathrm{2}\sqrt{{x}}{du} \\ $$$$\Rightarrow\:\Omega\:=\:\int\frac{\mathrm{2}\sqrt{{x}}{du}}{\left(\mathrm{1}+\sqrt{{u}}\right)\sqrt{{x}}}\:=\:\mathrm{2}\int\frac{{du}}{\left(\mathrm{1}+\sqrt{{u}}\right)} \\ $$$${t}=\sqrt{{u}}\:\rightarrow\:{t}^{\mathrm{2}} ={u}\:\rightarrow\:\mathrm{2}{tdt}={du} \\ $$$$\Rightarrow\:\Omega\:=\:\mathrm{2}\int\frac{\mathrm{2}{tdt}}{\left(\mathrm{1}+{t}\right)}\:=\:\mathrm{4}\int\frac{{t}+\mathrm{1}−\mathrm{1}}{\left(\mathrm{1}+{t}\right)}{dt} \\ $$$$\Rightarrow\:\Omega\:=\:\mathrm{4}\int{dt}−\mathrm{4}\int\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)}{dt} \\ $$$$\Rightarrow\:\Omega\:=\:\mathrm{4}{t}−\mathrm{4}{ln}\mid\mathrm{1}+{t}\mid+{C} \\ $$$$ \\ $$$$\Rightarrow\:\Omega\:=\:\mathrm{4}\sqrt{{u}}−\mathrm{4}{ln}\mid\mathrm{1}+\sqrt{{u}}\mid+{C} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\therefore\because\:\:\Omega\:=\:\mathrm{4}\left(\sqrt[{\mathrm{4}}]{{x}}\:−\:{ln}\mid\mathrm{1}+\sqrt[{\mathrm{4}}]{{x}}\mid+{C}\right. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:…………\mathscr{L}{e}\:{puissant}………… \\ $$
