Question Number 167360 by LEKOUMA last updated on 14/Mar/22
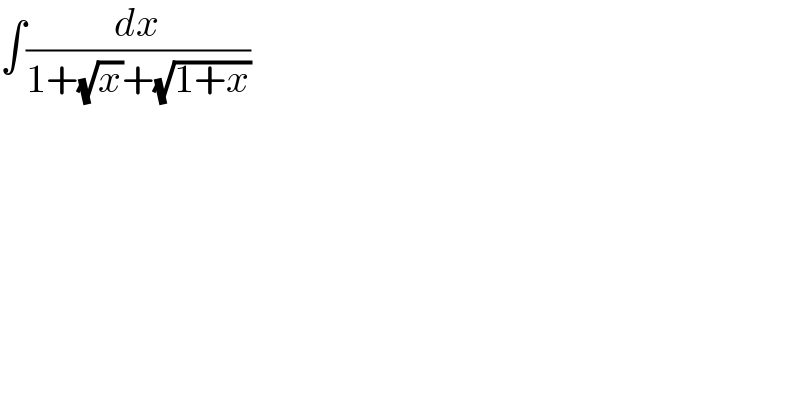
$$\int\frac{{dx}}{\mathrm{1}+\sqrt{{x}}+\sqrt{\mathrm{1}+{x}}} \\ $$
Answered by MJS_new last updated on 14/Mar/22
![∫(dx/(1+(√x)+(√(x+1))))= [t=(√x)+(√(x+1)) → dx=(((t−1)(t+1)(t^2 +1))/(2t^3 ))dt] =(1/2)∫(((t−1)(t^2 +1))/t^3 )dt= =(1/2)∫(1−(1/t)+(1/t^2 )−(1/t^3 ))dt= =(t/2)−(1/2)ln t −(1/(2t))+(1/(4t^2 ))= =((x+(2−(√(x+1)))(√x))/2)−(1/2)ln ((√x)+(√(x+1))) +C](https://www.tinkutara.com/question/Q167362.png)
$$\int\frac{{dx}}{\mathrm{1}+\sqrt{{x}}+\sqrt{{x}+\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{{x}}+\sqrt{{x}+\mathrm{1}}\:\rightarrow\:{dx}=\frac{\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{2}{t}^{\mathrm{3}} }{dt}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left({t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{{t}^{\mathrm{3}} }{dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{1}−\frac{\mathrm{1}}{{t}}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{{t}^{\mathrm{3}} }\right){dt}= \\ $$$$=\frac{{t}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:{t}\:−\frac{\mathrm{1}}{\mathrm{2}{t}}+\frac{\mathrm{1}}{\mathrm{4}{t}^{\mathrm{2}} }= \\ $$$$=\frac{{x}+\left(\mathrm{2}−\sqrt{{x}+\mathrm{1}}\right)\sqrt{{x}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\sqrt{{x}}+\sqrt{{x}+\mathrm{1}}\right)\:+{C} \\ $$
Commented by peter frank last updated on 14/Mar/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
